REFERÊNCIA:
http://opensadorselvagem.org/arquivo/cronicas-matematicas/os-problemas-matematicos-e-o-jogo-do-xadrez
http://ludicum.org/MR/textos/ArtigoSPM.pdf

A resolução de problemas de xadrez, como por exemplo, dar mate num ou dois lances, é utilizada como uma estratégia de aprendizagem e aperfeiçoamento dos jogadores de xadrez (Rocha, 2005).
Analisando alguns livros e sites relacionados ao xadrez é fácil verificar, que é comum o recurso à resolução de problemas.
Analisando alguns livros e sites relacionados ao xadrez é fácil verificar, que é comum o recurso à resolução de problemas.
Estes problemas baseiam-se nos finais de partida, nas aberturas e no jogo médio. Segundo Wood (1972) os problemas de xadrez apareceram por volta do ano 800. (em tumbas egípcias de aproximadamente 1500 a.C. foram encontrados indícios do jogo de xadrez) Este fato é corroborado pela historiadora Carmem Romero (2006), referindo que nos finais do século XVIII aparecem documentos onde são descritas coleções de problemas de xadrez. A utilização de problemas de xadrez já se encontrava fortemente presente no livro de Damiano, impresso em 1512, com 72 problemas. Nesta obra, Damiano escreve alguns conselhos que ainda são passados pelos professores de xadrez:
- nunca jogue rápido demais;
- se vires uma boa jogada procura por uma melhor,
- nunca jogue rápido demais;
- se vires uma boa jogada procura por uma melhor,
- nenhuma jogada deve ser feita ao acaso.
Relativamente ao primeiro conselho acima enunciado, um professor de xadrez mandava colocar as mãos debaixo da mesa no fim de cada jogada do adversário no sentido de obrigar os jogadores a pensarem melhor antes de tocarem na peça a jogar.
O movimento das peças de xadrez produz padrões específicos de cada peça e de acordo com a casa que ocupa no tabuleiro. Como exemplo. Apresentamos padrões formados pelo cavalo e pela dama, ou rainha (como alguns jogadores preferem chamar).
O movimento das peças de xadrez produz padrões específicos de cada peça e de acordo com a casa que ocupa no tabuleiro. Como exemplo. Apresentamos padrões formados pelo cavalo e pela dama, ou rainha (como alguns jogadores preferem chamar).
Estes padrões são muito úteis para uma mais rápida identificação da situação do jogo, ou seja, das possíveis jogadas de cada jogador.

Figura 1: Movimentos do cavalo e da dama (Retirado do site da FIDE)
O tabuleiro e as peças de xadrez têm sido utilizados na resolução de problemas muito interessantes, mas que não se reportam ao jogo em si. Neste tipo de problemas as peças de xadrez movimentam-se segundo as regras do xadrez e o tabuleiro pode assumir o formato do tabuleiro de xadrez 8x8 ou outros formatos, como 3x3, 4x4, nxn. O puzzle de xadrez mais antigo que se conhece data de 1512 e é conhecido por “Guarini’s Problem”(Watkins, 2004). Este problema consiste em trocar os cavalos brancos de lugar com os cavalos pretos, partindo das posições presentes na Figura 2
. 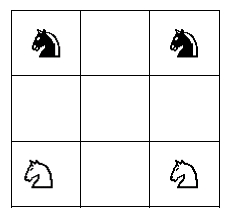

Figura 2 “Guarini´s Problem”
Há um problema matemático com os movimentos do cavalo que fascinou célebres matemáticos, como Leonard Euler. Neste problema o cavalo deve percorrer todas as casas do tabuleiro uma só vez. Se a casa de partida é diferente da casa de chegada, o problema diz-se aberto, se a casa de partida é coincidente com a casa de chegada, diz-se fechado.
Existem 122.000.000 soluções para a situação em que o cavalo regressa à casa de partida, havendo vários milhares de milhões de soluções no total. Euler foi o primeiro matemático a examinar e descrever este problema . Segundo Watkins (2004) os Knight's Tour Problem remontam quase ao início do xadrez, no século VI, na Índia.
Uma variante deste problema consiste em fazer o cavalo percorrer o maior caminho possível sem se cruzar. Estes problemas podem ser fechados ou abertos se o cavalo termina ou não na casa de partida e podem utilizar-se tabuleiros n x n casas (Figura 3).
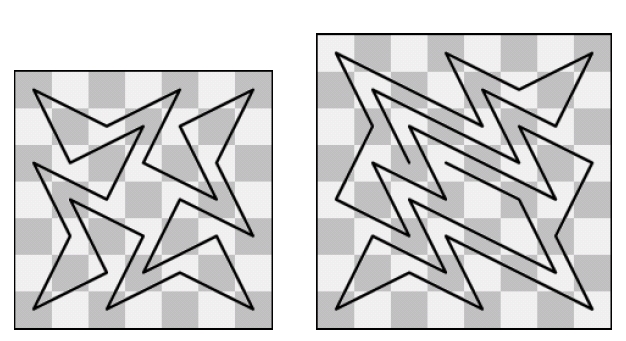
Figura 3: Volta do cavalo não cruzada em tabuleiro 7x7 e 8x8
A extensão deste tipo de problemas a outras dimensões é complexa, mas apresenta resultados muito interessantes. Um exemplo disso é a volta do cavalo num cubo.
Analisando o quadrado de Euler verifica-se que os 4 x 4 quadrados que formam o quadrado maior são também quadrados semi-mágicos cuja soma dos números de cada coluna ou linha perfaz 130. E a soma dos números dos quadrados 2 x 2 que os compõem também perfaz o mesmo número, 130 (Watkins, 2004).
Um problema adicional é o de conseguir que, ficando as casas numeradas de 1 a 64 com os movimentos sucessivos do cavalo no seu percurso, o quadrado com números seja um quadrado mágico, isto é, de modo que a soma em todas as linhas, colunas e diagonais principais sejam sempre a mesma. Euler tentou encontrar uma solução para este problema.
Analisando o quadrado de Euler verifica-se que os 4 x 4 quadrados que formam o quadrado maior são também quadrados semi-mágicos cuja soma dos números de cada coluna ou linha perfaz 130. E a soma dos números dos quadrados 2 x 2 que os compõem também perfaz o mesmo número, 130 (Watkins, 2004).
Um problema adicional é o de conseguir que, ficando as casas numeradas de 1 a 64 com os movimentos sucessivos do cavalo no seu percurso, o quadrado com números seja um quadrado mágico, isto é, de modo que a soma em todas as linhas, colunas e diagonais principais sejam sempre a mesma. Euler tentou encontrar uma solução para este problema.
Embora o quadrado seja semi-mágico. A soma dos números das colunas, assim como a soma dos números das linhas é 260. No entanto, o mesmo não acontece para as diagonais principais, daí não ser um quadrado mágico e sim um quadrado semi-mágico.
Este problema parece não ter solução para um quadrado de 8 x 8, como refere Weisstein (2003). No entanto, há exemplos de quadrados mágicos com a 'volta do cavalo' em tabuleiros de xadrez de 16 x 16, 20 x 20, 24 x 24,32 x 32, 48 x 48 e 64 x 64 quadrados (Watkins, 2004).
Este problema parece não ter solução para um quadrado de 8 x 8, como refere Weisstein (2003). No entanto, há exemplos de quadrados mágicos com a 'volta do cavalo' em tabuleiros de xadrez de 16 x 16, 20 x 20, 24 x 24,32 x 32, 48 x 48 e 64 x 64 quadrados (Watkins, 2004).
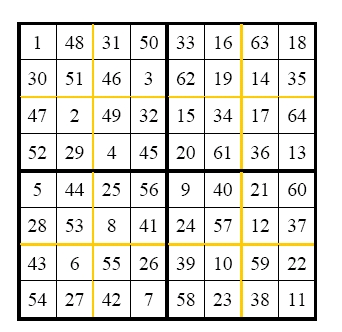
Figura 4: Quadrado semi-mágico com os movimentos do cavalo
Os quadrados mágicos têm seduzido diversos matemáticos e a sua construção ou identificação pode constituir uma atividade muito interessante como didática escolar. O quadrado mágico mais antigo que se conhece é o chinês "lo-shu" (Figura 5). Segundo a lenda, este quadrado terá sido trazido para os homens por uma tartaruga do rio Lo no reinado do imperador Yii (Boyer, 2002).
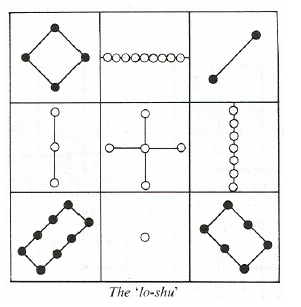
Figura 5: Quadrado mágico "lo-shu" (Retirado de Williams e Shuard, 1994, p. 281)
Para construir o "lo-shu", Yang Hui3 recomenda as seguintes três fases, iniciando da esquerda para a direita, como se pode observar na Figura 6.
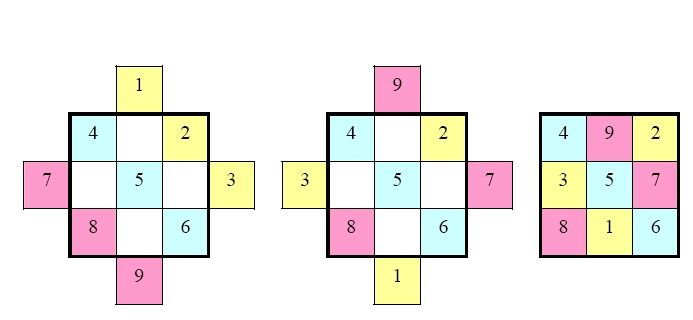

Figura 6: Construção do lu-shu (Adaptado de Estrada et al, 2000, p.171)
Na primeira fase são colocados os números de 1 a 9 de determinada maneira, na segunda fase faz-se o reordenamento e, por fim, o arranjo final.
O interesse pela construção de quadrados mágicos levou à construção dos quadrados mágicos Pitagóricos. Este problema consiste na construção de quadrados mágicos sobre os lados de um triângulo retângulo de forma a que a soma do quadrado dos números que compõem o quadrado formado sobre a hipotenusa seja igual à soma do quadrado dos números que compõem os quadrados formados sobre os restantes lados.
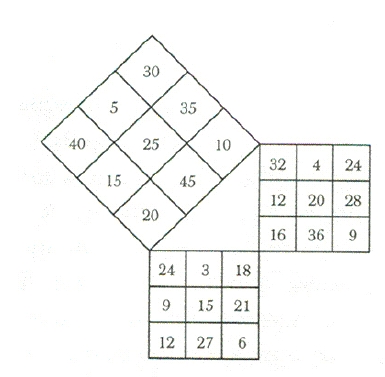
Figura 7: Quadrados mágicos Pitagóricos (Retirado de Pickover, 2002, p.105)
Watkins (2004) apresenta uma larga série de problemas, alguns dos quais são uma variante dos Knight's Tour Problem aplicados a outras peças de xadrez, como a dama, o bispo, a torre e o rei, onde se verificam padrões muito interessantes, quer em termos visuais quer em termos das suas implicações matemáticas.
À semelhança dos quadrados mágicos construídos com a volta do cavalo podem, de forma semelhante, ser construídos quadrados mágicos com outras peças, como o rei e a torre.
O grande matemático Karl Gauss interessou-se pelo problema que consistia em colocar oito damas no tabuleiro de modo que nenhuma se ataque. Calculou a existência de 92 posições para esse problema (Wood, 1972). No entanto, se retirarmos as simetrias e rotações apenas existem 12 soluções. O problema das oito damas foi inventado pelo jogador de xadrez alemão Max Bezzel em 1848, tornando-se um popular jogo de computador nos anos 90.

Figura 8: Problema das 5 e 8 damas (Retirado de Wood, 1972, p.108. Esquerda: damas colocadas de modo a atacarem todas as casas do tabuleiro; Direita: Problema das oito damas)
Outro problema com damas consiste em colocar 5 damas, ou o mínimo de damas possível de modo a que ataquem todas as casas do tabuleiro.
Petković (1997) refere diversas variantes de problemas com a dama para além de muitos outros envolvendo o jogo de xadrez ou apenas o tabuleiro e algumas peças.
Um problema relacionado com o crescimento exponencial utiliza os 64 quadrados do tabuleiro de xadrez. Baseia-se numa lenda em que Sissa, o inventor do xadrez, como pagamento pelo seu invento, pede um grão de trigo pelo primeiro quadrado, dois pelo segundo, quatro pelo terceiro, ou seja, em cada novo quadrado o dobro do quadrado precedente. Depressa verificaram a impossibilidade de fazer o pagamento. Só o 64.º quadrado necessitaria de 9.233.372.036.854.775.808 grãos e para o pagamento seriam necessários 18.446.744.073.709.551.615 grãos. Para termos uma idéia acerca do volume que esses grãos ocupariam, verificou-se que se vinte grãos encherem 1 cm3 serão necessários 20 milhões para encherem 1m3. Assim, os grãos que Sissa deveria receber ocupariam mais de 922.3373203.685 m3, o que daria para cobrir oito vezes a superfície da Terra.
Uma última informação interessante que eu não poderia deixar passar, é que o Xadrez é disciplina escolar obrigatória na Romênia e as notas em Matemática dependem em 33% do desempenho no Xadrez.
Petković (1997) refere diversas variantes de problemas com a dama para além de muitos outros envolvendo o jogo de xadrez ou apenas o tabuleiro e algumas peças.
Um problema relacionado com o crescimento exponencial utiliza os 64 quadrados do tabuleiro de xadrez. Baseia-se numa lenda em que Sissa, o inventor do xadrez, como pagamento pelo seu invento, pede um grão de trigo pelo primeiro quadrado, dois pelo segundo, quatro pelo terceiro, ou seja, em cada novo quadrado o dobro do quadrado precedente. Depressa verificaram a impossibilidade de fazer o pagamento. Só o 64.º quadrado necessitaria de 9.233.372.036.854.775.808 grãos e para o pagamento seriam necessários 18.446.744.073.709.551.615 grãos. Para termos uma idéia acerca do volume que esses grãos ocupariam, verificou-se que se vinte grãos encherem 1 cm3 serão necessários 20 milhões para encherem 1m3. Assim, os grãos que Sissa deveria receber ocupariam mais de 922.3373203.685 m3, o que daria para cobrir oito vezes a superfície da Terra.
Uma última informação interessante que eu não poderia deixar passar, é que o Xadrez é disciplina escolar obrigatória na Romênia e as notas em Matemática dependem em 33% do desempenho no Xadrez.
Figura 8: Problema das 5 e 8 damas (Retirado de Wood, 1972, p.108. Esquerda: damas colocadas de modo a
atacarem todas as casas do tabuleiro; Direita: Problema das oito damas)
Outro problema com damas consiste em colocar 5 damas, ou o mínimo de damas
possível de modo a que ataquem todas as casas do tabuleiro (Petković, 1997).
Petković (1997) refere diversas variantes de problemas com a dama para além de
muitos outros envolvendo o jogo de xadrez ou apenas o tabuleiro e algumas peças.
Um problema relacionado com o crescimento exponencial utiliza os 64 quadrados do
tabuleiro de xadrez. Baseia-se numa lenda em que Sissa, o inventor do xadrez, como
pagamento pelo seu invento, pede um grão de trigo pelo primeiro quadrado, dois pelo
segundo, quatro pelo terceiro, ou seja, em cada novo quadrado o dobro do quadrado
precedente. Depressa verificaram a impossibilidade de fazer o pagamento. Só o 64.º quadrado
necessitaria de 9.233.372.036.854.775.808 grãos e para o pagamento seriam necessários
18.446.744.073.709.551.615 grãos. Para termos uma ideia acerca do volume que esses grãos
ocupariam, verificou-se que se vinte grãos encherem 1 cm
3
serão necessários 20 milhões para
encherem 1m
3
. Assim, os grãos que Sissa deveria receber ocupariam mais de
922.3373203.685 m
3
, o que daria para cobrir oito vezes a superfície da Terra (Murray, 1913).







Nenhum comentário:
Postar um comentário