PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
CXSAJBA - CLUBE DE XADREZ SANTO ANTÔNIO DE JESUS, BAHIA. OUTRO BLOG DO CLUBE DE XADREZ: http://clubedexadrezsantoantoniodejesusbahia.blogspot.com


RESPEITE AS CRIANÇAS!

AS CRIANÇAS NÃO SÃO LIXO.




NÚMERO DE FOTOS E IMAGENS DESTE BLOG.
O CLUBE DE XADREZ SANTO ANTONIO DE JESUS, BAHIA (CXSAJBA) AGRADECE PELA VISITA, NESTE BLOG.
O NÚMERO DE FOTOS E IMAGENS, DESTE BLOG: 305.
O NÚMERO DE FOTOS E IMAGENS, DESTE BLOG: 305.
VISITANTE DE NÚMERO:
domingo, 15 de abril de 2012
TEXTO 123 - PARTE 27: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
Ao invés de lidar diretamente com os objetos, suas classes ou suas relações, a
composição combinatória refere-se a reuniões mais complexas e suas transformações.
Trata-se, por exemplo, de saber se duas características x e y se excluem (donde x y +
x y) ou são simplesmente disjuntivas, mas podem se
_ _
apresentar juntas (donde xy + x y + x y).
Nesse caso, o raciocínio do sujeito não se refere somente ao real, mas também ao real em função do possível. Efetivamente, a reunião (+) não é mais aqui uma adição de casos reais, pois não se podem sempre realizar-se simultaneamente, mas uma reunião dos possíveis, e é por isso que a operação fundamental da lógica das proposições é indicada por v no sentido de “ou”; x v y significa assim
(e é a significação que a reunião das associações possíveis adquire no espírito do sujeito), “ou xy é verdadeiro, ou x y , ou x y, ou dois desses casos em três, ou todos os três, o que significa que a expressão x v y é uma de 7 possibilidades. (INHELDER; PIAGET, 1955, p. 218-219).
Finalmente, a composição combinatória refere-se a proposições. Desde as operações concretas (e mesmo desde o nível pré-operatório), o raciocínio baseia-se nas proposições, com ou sem a presença perceptiva dos objetos descritos. Mas a operação concreta consiste em decompor e recompor o conteúdo dessas proposições, ou seja, as classes e relações em jogo na matéria concreta da proposição: assim, uma proposição ainda não é, no período concreto, ligada a uma outra enquanto proposição, mas unicamente graças a seu conteúdo lógico que consiste de estruturas de classes e
relações em correspondência com os objetos.
(...) logo que ingressa no caminho de uma coordenação dos agrupamentos concretos num sistema único (na segunda potência), o pensamento se torna formal porque se refere às combinações possíveis e não mais aos objetos em si. Por mais tateantes e incompletas que sejam, a esse respeito, as primeiras tentativas do pensamento no início do estádio III [formal], o pensamento se orienta para uma nova forma de equilíbrio, caracterizado por uma nova estrutura de conjunto que deriva ao mesmo tempo do reticulado e do grupo das
inversões e reciprocidades. (INHELDER; PIAGET, 1955, p. 219).
Depois de descrever a passagem das operações concretas às formais ou proposicionais, Piaget (1949, p. 208-222) apresenta as 16 operações binárias da lógica das proposições, que o sujeito do período formal faz uso.
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
Ao invés de lidar diretamente com os objetos, suas classes ou suas relações, a
composição combinatória refere-se a reuniões mais complexas e suas transformações.
Trata-se, por exemplo, de saber se duas características x e y se excluem (donde x y +
x y) ou são simplesmente disjuntivas, mas podem se
_ _
apresentar juntas (donde xy + x y + x y).
Nesse caso, o raciocínio do sujeito não se refere somente ao real, mas também ao real em função do possível. Efetivamente, a reunião (+) não é mais aqui uma adição de casos reais, pois não se podem sempre realizar-se simultaneamente, mas uma reunião dos possíveis, e é por isso que a operação fundamental da lógica das proposições é indicada por v no sentido de “ou”; x v y significa assim
(e é a significação que a reunião das associações possíveis adquire no espírito do sujeito), “ou xy é verdadeiro, ou x y , ou x y, ou dois desses casos em três, ou todos os três, o que significa que a expressão x v y é uma de 7 possibilidades. (INHELDER; PIAGET, 1955, p. 218-219).
Finalmente, a composição combinatória refere-se a proposições. Desde as operações concretas (e mesmo desde o nível pré-operatório), o raciocínio baseia-se nas proposições, com ou sem a presença perceptiva dos objetos descritos. Mas a operação concreta consiste em decompor e recompor o conteúdo dessas proposições, ou seja, as classes e relações em jogo na matéria concreta da proposição: assim, uma proposição ainda não é, no período concreto, ligada a uma outra enquanto proposição, mas unicamente graças a seu conteúdo lógico que consiste de estruturas de classes e
relações em correspondência com os objetos.
(...) logo que ingressa no caminho de uma coordenação dos agrupamentos concretos num sistema único (na segunda potência), o pensamento se torna formal porque se refere às combinações possíveis e não mais aos objetos em si. Por mais tateantes e incompletas que sejam, a esse respeito, as primeiras tentativas do pensamento no início do estádio III [formal], o pensamento se orienta para uma nova forma de equilíbrio, caracterizado por uma nova estrutura de conjunto que deriva ao mesmo tempo do reticulado e do grupo das
inversões e reciprocidades. (INHELDER; PIAGET, 1955, p. 219).
Depois de descrever a passagem das operações concretas às formais ou proposicionais, Piaget (1949, p. 208-222) apresenta as 16 operações binárias da lógica das proposições, que o sujeito do período formal faz uso.
TEXTO 122 - PARTE 26: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
4.4 A INTELIGÊNCIA OPERATÓRIA FORMAL
Para Inhelder e Piaget (1955, p. 183-184), o estudo do desenvolvimento psicológico do pensamento pode ser feito em dois pontos de vista complementares: o das condições de equilíbrio e o das condições das estruturas. Do ponto de vista das condições de equilibro, o pensamento parece, em cada uma das suas formas, passar de estados menos equilibrados a estados mais equilibrados, sendo possível identificar
dois fatores principais relativos à essa equilibração pior ou melhor: um relativo à
extensão maior ou menor do campo do equilíbrio, e o outro aos instrumentos de
coordenação, ou seja, às estruturas de que a inteligência dispõe nos níveis
considerados.
Do ponto de vista das condições das estruturas, o problema consiste em
verificar a filiação das estruturas que caracterizam essas coordenações, assim como
seu modo de construção. Essa construção depende de três fatores principais: a
maturação do sistema nervoso, a experiência adquirida em função do meio físico, e a
ação do meio social. No entanto, Piaget destaca que estes fatores só atuam, respectiva
e concorrentemente, ao se submeterem às leis de equilíbrio que determinam as
melhores formas de adaptação compatíveis com o conjunto das condições em jogo.
“Portanto, o equilíbrio e a estrutura são os dois aspectos complementares de toda
organização do pensamento.” (INHELDER; PIAGET, 1955, p. 184).
4.4.1 O pensamento formal do ponto de vista do equilíbrio
Inhelder e Piaget (1955, p. 185) destacam que a principal característica do
pensamento formal está ligada ao papel que dá ao possível com relação às verificações
de realidade, e que comparado ao pensamento concreto, constitui uma nova forma de
equilíbrio.
Ao final do período sensório-motor, por intermédio da função simbólica, uma
nova forma de pensamento se desenvolve na criança. Esta forma de pensamento é de
natureza pré-lógica (ou pré-operatória) e difere do pensamento operatório concreto sob
três aspectos: primeiro, ao considerar situações estáticas, a criança tende a explicá-las
em função de seus caracteres de configuração atual, mais do que em função das
transformações que levam de uma situação a outra. Segundo, o pensamento do sujeito,
no que se refere a essas transformações, assimila-as às ações pessoais do sujeito e
não a operações reversíveis. Estas duas diferenças podem ser reduzidas a uma: os
estados e as modificações ainda não formam, no nível do pensamento intuitivo, um sistema único, enquanto que no nível das operações concretas as situações se
subordinarão às transformações em si mesmas. Terceiro, já existe neste nível uma
tendência para a formação de sistemas de conjunto, mas a reversibilidade neste
período é ainda incompleta. (INHELDER; PIAGET, 1955, p. 185-186).
Já com o surgimento do pensamento concreto, o sistema das regulações, até
então sem estabilidade, chega a uma primeira forma de equilíbrio estável:
(...) ao atingir o nível da reversibilidade completa, as operações concretas
decorrentes das regulações precedentes se coordenam, na realidade, em
estruturas definidas (classificações, seriações, correspondências, etc.) que se
conservarão durante toda a vida, sem excluir a formação de sistemas
superiores, mas continuando ativos no plano limitado da organização dos dados
imediatos. (INHELDER; PIAGET, 1955, p. 187).
Esta forma de equilíbrio consiste, em primeiro lugar, em que os domínios
sucessivamente estruturados por esse pensamento concreto não admitem mais
oposição entre as situações estáticas e as transformações, sendo que as primeiras
subordinam-se às segundas, no sentido em que cada estado é concebido como
resultado de uma transformação.
Em segundo lugar, afirmar que o sistema das transformações está em equilíbrio
significa dizer que essas transformações adquiriram uma forma reversível e a
potencialidade para se coordenar segundo as leis fixas da composição, sendo que as
transformações são agora assimiladas às operações.
Em terceiro lugar, o pensamento operatório concreto, comparado ao
pensamento intuitivo pré-operatório, caracteriza-se por uma extensão do real na direção
do virtual, pois classificar objetos significa construir conjuntos de tal forma que novos
objetos possam ser ligados aos objetos já classificados, e novas inclusões se tornem
possíveis. Da mesma forma, seriar objetos em ordem comporta novas subdivisões
possíveis, mas estas possibilidades intrínsecas às operações concretas não estão
ainda abertas para um campo mais ou menos amplo de hipóteses, como será o caso
das operações formais. (INHELDER; PIAGET, 1955, p. 187).
(...) o pensamento concreto continua fundamentalmente ligado ao real, e o
sistema das operações concretas, que constitui a forma final de equilíbrio do
pensamento intuitivo, chega apenas a um conjunto restrito de transformações
virtuais, e, portanto, a uma noção do “possível” que é apenas uma extensão
(não muito grande) do real. Este caráter do pensamento concreto é muito claro
(...) [ao se comparar] o pensamento concreto da criança ao pensamento formal
do pré-adolescente ou do adolescente; enquanto que estes últimos, para
resolver o problema que lhes é proposto, começam imediatamente a construir
um conjunto de hipóteses entre as quais precisarão escolher
experimentalmente a melhor, a criança do nível concreto a rigor não cria
hipóteses. Age desde o começo, e apenas procura, durante sua ação,
coordenar as leituras sucessivas dos resultados que obtém, o que significa
estruturar a realidade na qual atua. Ou, se admitimos que cria hipóteses, é
preciso esclarecer que estas são apenas projetos de ações possíveis, e não,
como no adolescente, formas de imaginar o que deveria ser o real se tal ou qual
condição hipotética fosse satisfeita. (INHELDER; PIAGET, 1955, p. 188).
Inhelder e Piaget (1955, p. 189-191) apontam quatro características do
pensamento formal: inversão de sentido entre o real e o possível, o que faz com que o
pensamento formal seja essencialmente hipotético-dedutivo. O pensamento formal
refere-se a elementos verbais, e não mais diretamente aos objetos. O pensamento
formal constitui um sistema de operações de segunda potência. E por último a
utilização de um procedimento combinatório.
Com o pensamento formal ocorre uma inversão de sentido entre o real e o
possível, pois em vez de o possível se manifestar simplesmente sob a forma de um
prolongamento do real ou das ações executadas na realidade, é, ao contrário, o real
que se subordina ao possível. No pensamento formal, os fatos são concebidos como o
setor das realizações efetivas no meio de um universo de transformações possíveis,
pois não são explicados, e nem admitidos como fatos, senão depois de uma verificação
que se refere ao conjunto das hipóteses compatíveis com a situação dada.
É esta inversão de sentido entre o real e o possível que, mais que qualquer
outra propriedade subseqüente, caracteriza o pensamento formal: em vez de
apenas introduzir um início de necessidade no real, como ocorre nas
inferências concretas, realiza desde o início a síntese entre o possível e o
necessário, deduzindo com rigor as conclusões de premissas, cuja verdade
inicialmente é admitida apenas por hipótese, e, assim, vai do possível para o real. (INHELDER; PIAGET, 1955, p. 189).
Dessa forma, o pensamento formal é essencialmente hipotético-dedutivo, sendo
que a dedução não mais se refere a realidades percebidas, mas a enunciados
hipotéticos, isto é, a proposições que se referem a hipóteses ou apresentam dados
apenas como simples dados, independente do seu caráter real. Assim, a dedução
consiste em ligar estas suposições, e delas deduzir suas conseqüências necessárias,
mesmo quando sua verdade experimental não ultrapassa o possível. (INHELDER;
PIAGET, 1955, p. 189).
O pensamento formal também possui a propriedade de referir-se a elementos
verbais, e não mais diretamente aos objetos, embora nem todo pensamento verbal seja
formal. Quando os objetos são substituídos por enunciados verbais, superpõe-se uma
nova lógica – a das proposições – à das classes e relações que se referem a esses
objetos, e esta é uma segunda propriedade fundamental do pensamento formal. E esta
lógica das proposições comporta um número bem maior de possibilidades operatórias
do que os simples agrupamentos de classes e de relações. Assim, é o número de
operações possíveis que, inicialmente, a distingue funcionalmente do pensamento
concreto, pois, a prova disso é que a lógica das proposições se manifesta sob suas
formas mais características, tanto diante de situações experimentais, como diante de
problemas puramente verbais. (INHELDER; PIAGET, 1955, p. 190).
Inhelder e Piaget (1955, p. 190) destacam que o papel do pensamento formal
não se reduz a traduzir em palavras ou em proposições o que poderia ter sido
executado concretamente sem o seu recurso. Ao contrário, é durante as manipulações
experimentais que se afirma, no início do pensamento formal, uma série de
possibilidades operatórias novas, formadas por disjunções, implicações, exclusões, etc.,
que intervêm desde a organização da experiência e desde a leitura dos dados de fato.
A razão disso é que desde o contato com os problemas de fato, o pensamento formal
parte da hipótese, ou seja, do possível, em vez de limitar-se a uma estruturação direta
dos dados percebidos.
Assim, o característico da lógica das proposições não é ser uma lógica verbal.
É, antes de tudo, uma lógica de todas as combinações possíveis do pensamento, tanto
no caso em que tais combinações aparecem com problemas experimentais, quanto no caso em que aparecem diante de problemas puramente verbais.
E o motor efetivo da lógica das proposições é o poder de combinar, graças ao
qual ela insere o real no conjunto das hipóteses possíveis, compatíveis com os dados.
Inhelder e Piaget (1955, p. 190-191) destacam ainda que o pensamento formal
se constitui num sistema de operações de segunda potência. As operações concretas
são as operações de primeira potência, pois se referem diretamente aos objetos, como
por exemplo, a construção de relações entre elementos dados. No entanto, também é
possível construir relações entre relações, como por exemplo, as proporções, cuja
conquista só é obtida no nível formal, sendo que as proporções supõe as operações de
segunda potência.
Esta noção de operação de segunda potência exprime novamente o caráter
geral do pensamento formal, que é o de ultrapassar o quadro das
transformações que se referem diretamente ao real (operações de primeira
potência) subordinando-as a um sistema de combinações hipotético-dedutivas,
e, portanto, simplesmente possíveis. (INHELDER; PIAGET, 1955, p. 191).
Por fim, Inhelder e Piaget destacam o caráter combinatório do pensamento
formal, pois para lidar com o possível, o sujeito precisa de um instrumento para gerá-lo,
e esse instrumento é uma combinatória, um procedimento para combinar elementos
que, diante de uma situação determinada, permite ao sujeito a produção de todos os
casos possíveis. Inhelder e Piaget afirmam que “apenas uma combinação dá o conjunto
dos possíveis e, no terreno experimental, a pesquisa das combinações novas é
precisamente o que caracteriza a hipótese.” (1955, p. 191). Ver quadro 24.
QUADRO 24 – CARACTERÍSTICAS DO PENSAMENTO FORMAL.
Do ponto de vista físico, sabe-se que um estado de equilíbrio se caracteriza pela compensação entre todas as modificações virtuais, compatíveis com as ligações
do sistema considerado. No dizer de Inhelder e Piaget (1955, p. 193):
(...) para conceber o possível, o pensamento formal é obrigado a dispor, em cada situação específica, de uma grande amplitude de operações virtuais que ultrapassam o domínio das operações momentaneamente utilizadas de fato, e
tais operações virtuais constituem uma condição necessária de equilíbrio, e isso, pelas duas razões seguintes: de um lado, são elas que correspondem ao que na linguagem da teoria do equilíbrio, denominamos as “transformações virtuais”; de outro, há equilíbrio na medida em que essas transformações virtuais “se
compensam” exatamente, ou, na linguagem das operações, na medida em que tais operações possíveis constituem um sistema rigorosamente reversível do
ponto de vista lógico.
Do ponto de vista lógico, a significação lógica representa um caráter indispensável para o funcionamento do pensamento hipotético-dedutivo ou formal.
Deve-se ter em mente que, na realidade, o possível formal é o correlato obrigatório, de noção e de necessidade.
Inhelder e Piaget (1955, p. 193) destacam que:
Uma afirmação relativa apenas ao real – por exemplo, um juízo de existência ou um juízo predicativo – não precisa ser necessário: a afirmação é verdadeira ou falsa, na medida em que corresponde ou não a um fato. Uma dedução que refere a uma hipótese (ou a um dado de fato, mas admitido como hipótese), é, ao contrário, necessariamente verdadeira, do ponto de vista formal, desde que seja correta, e isso independentemente do valor da hipótese admitida. A
conexão marcada pelas palavras “se...então” (implicação inferencial) consiste em ligar uma conseqüência necessária a uma afirmação simplesmente possível: é esta síntese do necessário e do possível que caracteriza o emprego desse possível no pensamento formal, por oposição ao possível extensão-doreal do pensamento concreto e às possibilidades não reguladas, características das ficções da imaginação.
Inhelder e Piaget (1955, p. 193-194), ao indagar em que consiste este possível formal, argumentam “é possível tudo que não é contraditório”. Assim, a reversibilidade operatória formal que, na perspectiva física significa a exata compreensão das transformações (ou operações) virtuais, adquire na perspectiva lógica, a significação da
necessidade dedutiva.
No conjunto, esses dois aspectos, físico e lógico, da noção de possível,
psicologicamente constituem apenas um: ao situar um estado real num sistema
de transformações possíveis, o pensamento formal assegura, simultaneamente,
seu equilíbrio, do ponto de vista da conservação psicológico ulterior das
estruturas que desenvolve, e seu valor de instrumento lógico necessário, do
ponto de vista da utilização dessas estruturas, enquanto instrumentos
dedutivos. (INHELDER; PIAGET, 1955, p. 194).
Inhelder e Piaget (1955, p. 195) apontam duas significações psicológicas para a
palavra possível: o materialmente possível e o estruturalmente possível. O
materialmente possível é o possível do ponto de vista do sujeito, e refere-se às
operações ou relações que o sujeito concebe como possível, ou seja, aquilo que o
sujeito sabe que pode efetuar ou construir, mesmo que não o faça efetivamente. O
estruturalmente possível é o possível do ponto de vista do observador, e são as
operações e relações que o sujeito seria capaz de efetuar ou de construir, mas sem que
pense fazê-lo, ou seja, sem que tome consciência dessa eventualidade, nem de sua
capacidade a respeito. Inhelder e Piaget (1955, p. 196) destacam que:
(...) sempre devem ser consideradas, num ato de inteligência, as operações
reais, no sentido de efetivamente realizadas no pensamento consciente do
sujeito, e as operações “estruturalmente possíveis”, isto é, que não efetua, mas
que poderia efetuar. (...) é esse possível relativo às estruturas operatórias, de
que o sujeito dispõe, que constitui o possível do ponto de vista do observador e
que, portanto, corresponde, no domínio físico, às transformações virtuais, não
efetivamente realizadas.
O materialmente possível tem estreitas relações com o estruturalmente
possível, do qual constitui um primeiro plano de atualização: é na medida em que o
sujeito dispõe de um número suficiente de operações estruturalmente possíveis que
chega a imaginar as transformações materialmente possíveis. No dizer de Inhelder e
Piaget:
Sem um certo jogo de possibilidades estruturais (e é o que se manifesta
claramente ao nível pré-operatório, e mesmo no das operações concretas), não
poderia verificar os estados de fatos percebidos no real, os estados estáticos ou
as transformações atuais, e não chegaria a ter uma representação das
transformações hipotéticas que servem para que imagine novas experiências.
Portanto, o materialmente possível depende do estruturalmente possível.
(INHELDER; PIAGET, 1955, p. 196).
114
4.4.2 O pensamento formal do ponto de vista das Estruturas
Depois de caracterizar a diferença entre o pensamento concreto e pensamento
formal do ponto de vista do equilíbrio, por intermédio da extensão progressiva do
conjunto das operações virtuais ou possíveis, Inhelder e Piaget destacam que é
necessário comparar as estruturas totais que correspondem a essas duas formas de
equilíbrio.
Inhelder e Piaget (1955, p. 205) afirmam que todo estado de equilíbrio pode ser
reconhecido por uma certa forma de reversibilidade. Do ponto de vista estrutural, a
reversibilidade, que é a possibilidade permanente de uma volta ao ponto de partida, se
apresenta sob duas formas distintas e complementares. Pode-se voltar ao ponto de
partida anulando-se a operação efetuada, o que constitui uma inversão ou negação: o
produto da operação direta e de seu inverso é a operação nula ou idêntica. Mas
também se pode voltar ao ponto de partida anulando uma diferença (no sentido lógico
do termo), o que constitui uma reciprocidade: o produto de duas operações recíprocas
é, não uma operação nula, mas uma equivalência.
A inversão e a reciprocidade são encontradas sob aspectos diferentes em todos
os estádios de desenvolvimento, pois constituem as condições de equilíbrio das
ações mais elementares, bem como das ações superiores. É assim que no nível
perceptivo (embora não exista ainda nenhuma reversibilidade completa) as
inversões correspondem às adjunções ou supressões de elementos e as
reciprocidades às simetrias ou semelhanças. (INHELDER; PIAGET, 1955, p.
205).
Existe uma primeira diferença importante entre as estruturas concretas e
formais: enquanto que as segundas chegam a reunir as inversões e as reciprocidades
em um sistema único de transformações (o grupo INRC), os sistemas característicos
das operações concretas, ou agrupamentos de classes e de relações, decorrem da
inversão (classes) ou da reciprocidade (relações), sem síntese geral dessas duas
formas de reversibilidade. (INHELDER; PIAGET, 1955, p. 205-206).
115
De uma maneira geral, os “agrupamentos” elementares, que constituem as
únicas estruturas de conjunto acessíveis ao nível das operações concretas, se
caracterizam, portanto, por duas particularidades essenciais que as opõe às
estruturas formais: 1) Constituem sistemas de inclusões ou de encadeamentos
simples ou múltiplos, mas sem combinatória que inclua uma combinatória que
ligue os diversos elementos de n por n; por conseguinte não atingem a estrutura
do reticulado que comporta uma tal combinatória (“conjunto das partes”), mas
permanecem no estado de semi-reticulados; 2) Apresentam uma reversibilidade
que consiste seja em inversão (classes), seja em reciprocidade (relações), mas
não chegam a reunir essas duas formas de reversibilidade num sistema único;
por isso, não coincidem com a estrutura do grupo das inversões e
reciprocidades (o grupo INRC) e permanecem no estado de grupos
incompletos. (INHELDER; PIAGET, 1955, p. 207).
As estruturas concretas de classes consistem exclusivamente de classificações
simples (aditivas) ou multiplicativas (tabelas multiplicativas ou matrizes), de tal forma
que cada classe depende daquelas de que faz parte (A incluído em B, B em C, etc.) e
se opõe à sua complementar com relação à classe imediatamente superior (A‟ = B – A :
B‟ = C – B; etc.), mas sem combinatória que dê todos os sub-conjuntos possíveis de
classes no interior do sistema. Essas estruturas repousam exclusivamente na
reversibilidade por inversão: o sujeito pode assim reunir duas classes contíguas numa
única classe (A + A‟ = B; etc.) ou subtrair uma do todo assim formado (A = B – A‟); pode
também multiplicar uma classe pela outra (A1 x A2 = A1A2) ou abstrair uma do todo
assim formado (A1A2 : A2 = A1); mas tais sistemas ignoram a forma geral da
reciprocidade. (INHELDER; PIAGET, 1955, p. 206).
Inhelder e Piaget afirmam que as estruturas concretas de relações coordenam
entre si as equivalências completas (igualdades) ou parciais (alteridades) no caso de
relações simétricas, as diferenças ordenadas no caso das relações assimétricas
transitivas (seriações ou encadeamentos) e comportam igualmente os sistemas
multiplicativos (correspondências, etc.). A reversibilidade característica dessas
estruturas consiste de reciprocidades.
Para se entender a capacidade da inteligência operatória formal convém
compará-la com os agrupamentos mais complexos de que a inteligência operatória
concreta é capaz: as classificações multiplicativas (matrizes). Piaget e Inhelder (1959,
p. 188) fornecem o exemplo: dado um jogo de elementos de duplas características
(quadrados e círculos, vermelhos e azuis) que podem ser repartidos em duas classes
116
A1 e A‟1, segundo uma das suas características (A1= quadrados e A‟1= círculos) e,
igualmente, em duas classes A2 e A‟2, segundo a outra característica (A2= vermelhos e
A‟2= azuis), chama-se B1 à reunião das duas primeiras classes (formas), ou seja, B1= A1
+ A‟1, e B2 à reunião das duas segundas (cores), ou seja, B2= A2 + A‟2.
A classificação multiplicativa consiste em classificar esses elementos ao mesmo
tempo, segundo a classificação aditiva B1 e segundo a classificação aditiva B2, o que
originará quatro classes distintas: A1 A2+ A1 A‟2 + A‟1 A2 + A‟1 A‟2. Para resolver o
problema o sujeito deve, necessariamente, construir uma matriz de duas dimensões
(quadro de dupla entrada m n), como pode ser visto a seguir:
QUADRO 25 – MATRIZ DE DUPLA ENTRADA.
(...) o que falta às estruturas concretas de agrupamento é a combinatória intrínseca à construção do “conjunto das partes”, ou, o que é a mesma coisa, é a utilização de operações proposicionais (implicação, etc.) ou isomórficas
destas últimas, pois as operações interproposicionais repousam sobre a estrutura desse “conjunto das partes”. A diferença entre os agrupamentos elementares de classes e de relações (classificações, seriações e correspondências multiplicativas) e esta estrutura é que os primeiros constituem somente remi-reticulados, enquanto que o conjunto das partes forma um reticulado completo. Em segundo lugar, as operações com o “conjunto das partes” comportam uma inversa e uma recíproca: a segunda diferença essencial
entre os agrupamentos concretos e o sistema de operações formais refere-se, então, à ausência de um grupo único que ligue as inversões e reciprocidades nos agrupamentos elementares, bem como a presença desse grupo logo que se constitui o “conjunto das partes”. (INHELDER; PIAGET, 1955, p. 207).
Inhelder e Piaget destacam que não é suficiente assinalar estas diferenças entre as operações concretas e formais, mas de compreender o que leva o sujeito, por volta de 11 ou 12 anos, a construir efetivamente os “conjuntos das partes”. Com o objetivo de identificar em que casos os sujeitos utilizavam ou não as operações proposicionais, Inhelder e Piaget afirmam que “é quase impossível, diante de um
enunciado isolado qualquer, decidir entre essas duas possibilidades, e a questão não apresenta significação psicológica a não ser em função do conjunto dos raciocínios do sujeito ou de uma seqüência suficientemente sistemáticas de inferências.” Portanto, a linguagem dos sujeitos não traduz, senão de uma maneira muito aproximada, a estrutura real de seus pensamentos. (INHELDER; PIAGET, 1955, p. 209-210).
Inhelder e Piaget (1955, p. 210) propõem que é mais adequado comparar todos os enunciados, e, sobretudo todas as ações de um mesmo sujeito. Assim, pode-se ver se o sujeito se limita a uma simples leitura dos resultados brutos da experiência para destes extrair apenas classificações, seriações ou correspondências, ou se tenta dissociar os fatores, o que implica, ao mesmo tempo, um raciocínio hipotético-dedutivo
e uma combinatória.
Inhelder e Piaget destacam que a passagem das operações concretas para as operações formais não ocorre por um salto brusco, mas sim por múltiplas transições que o sujeito vai passar desde o nível da simples leitura dos fatos brutos, por meio de classificações, seriações e correspondências, para o nível da combinatória. Ao indagar sobre por que o equilíbrio final das operações combinatórias é tão
tardio, Inhelder e Piaget afirmam que:
(...) na medida em que as operações derivam umas das outras por coordenações progressivas, e em que as mais simples procedem da ação irreversível, compreendemos as razões pelas quais o equilíbrio das operações
combinatórias é tão tardio: o sujeito deve, inicialmente, dessubjetivar suas
ações para torná-las reversíveis, o que equivale a coordená-las em agrupamentos elementares ainda próximos da manipulação, e depois, como não consegue imediatamente dissociar inteiramente a forma e o conteúdo, é obrigado a reconstruir esses diversos agrupamentos nos domínios heterogêneos sucessivos que lhe impõe a experiência; é somente depois dessa estruturação progressiva dos diferentes conteúdos da experiência que um mecanismo formal geral começa a ser isolado por coordenação de conjunto. (INHELDER; PIAGET, 1955, p. 211).
Inhelder e Piaget destacam que enquanto as operações concretas procedem conteúdo por conteúdo, a realidade cedo ou tarde impõe uma mistura de conteúdos, forjando novos instrumentos operatórios. Dois métodos são então empregados pelo sujeito: no primeiro, o sujeito procura coordenar entre si os resultados das operações concretas, ou seja, eliminar as contradições aparentes; no segundo, o sujeito procura
coordenar diretamente entre si as diversas operações características dos agrupamentos concretos. Inhelder e Piaget assinalam que esses dois métodos conduzem à
descoberta da lógica formal das proposições, que consistem em: 1) Dissociar os conteúdos estruturados apenas pelas operações concretas, de maneira a coordenar os resultados dessas operações, em função das diversas combinações possíveis; 2) Coordenar os diversos agrupamentos de classes e de relações num único sistema total. Esses dois processos, por mais diferentes que possam parecer entre si, na realidade se reduzem a um só, pois os dois repousam numa combinatória. (INHELDER; PIAGET, 1955, p. 212).
No nível das operações concretas o sujeito procura estruturar a realidade de maneira mais completa que lhe é acessível, mas se limita ao real sob sua forma bruta.
A razão para isso é que as operações concretas (entre os 7 e 12 anos) têm por função estruturar o real, domínio por domínio, considerando esses conteúdos um após o outro,
às vezes com intervalo de alguns anos entre eles, como no caso das decalagens.
(...) quanto mais o sujeito analisa concretamente (portanto por simples correspondências entre os conteúdos distintos) a realidade, mais esta lhe apresenta misturas de regularidades parciais e exceções, e que não podem ser interpretadas com segurança. Inicialmente, é natural que o sujeito despreze,
seja as regularidades parciais, seja, principalmente, as exceções; mas, quando começa a levar a sério as exigências da experiência, encontra-se diante de uma situação sem saída do ponto de vista da simples descrição concreta dos fatos
brutos. (INHELDER; PIAGET, 1955, p. 213).
Inhelder e Piaget destacam que, cedo ou tarde, se impõe uma nova atitude experimental, que se pronuncia em numerosos casos desde o nível concreto, mas não
se generaliza antes do nível formal: é a tentativa de dissociar os fatores. Para compreender em que consiste essa tentativa de dissociar os fatores, deve-se analisar:
sob que formas nasce essa tentativa; sob que formas se generaliza e porque se generaliza tardiamente; como conduz necessariamente a uma combinatória. (INHELDER; PIAGET, 1955, p. 213).
No nível concreto, já existem algumas formas de dissociação de fatores, pois, tratando de decidir se determinado fator desempenha um papel ou não no resultado dado, o sujeito desse nível já é capaz de alguns processos, alguns por observação pura, outros por experimentação. Inhelder e Piaget informam que nesses dois casos (observação ou experimentação), a dissociação dos fatores, característica do nível concreto, é uma dissociação por negação, ou seja, o fator cujo papel é discutido às vezes está presente, às vezes ausente (observação) ou então é introduzido ou afastado
(experimentação). Portanto, tem-se aí exclusivamente transformações por inversão ou negação, e não reciprocidades; assim, tem-se a primeira e não as duas formas de reversibilidade.
Uma segunda diferença entre as dissociações elementares do nível das operações concretas e a dissociação do nível das operações formais é que, no caso de
dois ou vários fatores, x, y, etc., o sujeito não introduz e nem elimina o fator x a não ser para ver se desempenha sozinho um papel ativo, e não para estudar as variações de y.
Os sujeitos do nível formal, ao contrário, afastarão um fator x, e não somente para controlar sua influência, mas também para analisar a de y, sem perturbação por parte
de x. (INHELDER; PIAGET, 1955, p. 213-214).
As duas descobertas características do início do nível formal são que o sujeito pode dissociar fatores por neutralização, assim como por exclusão, e que é necessário
afastar um fator, não somente para analisar sua ação, mas ainda para mostrar a de outros fatores presentes. No dizer de Inhelder e Piaget:
É então que aparece a conduta característica do nível III [formal], que consiste em, diante de associações x, y, afastar y para estudar x sem interferências
perturbadoras, e reciprocamente. Portanto, a necessidade de excluir um fator para fazer variar um outro nasce de uma inversão de sentido na construção de correspondências, tendendo a abstrair ou a dissociar, em vez de multiplicar ou
associar, e isso diante da excessiva complexidade e das contradições que caracterizam a experiência bruta. Diante disso, alguns fatores podem ser afastados por inversão ou negação, mas isso não ocorre com todos. A segunda novidade característica do estádio III consiste em generalizar esta exclusão dos fatores perturbadores no caso em que tais fatores não comportam negação: neste caso o que é negado não é mais um dos termos (propriedade ou acontecimento), mas a diferença entre eles. Em outras palavras, o fator que
deve ser excluído é simplesmente neutralizado por igualização dos termos existentes, o que constitui uma reciprocidade, e não mais uma inversão. (INHELDER; PIAGET, 1955, p. 214-215).
Inhelder e Piaget afirmam que a dissociação de fatores, característica do nível formal, introduz uma reversibilidade por reciprocidade, ao mesmo tempo que por inversão, ao utilizar, de maneira paralela, as duas formas de reversibilidade, e ao tornálas funcionalmente equivalentes.
Inhelder e Piaget destacam que ainda é necessário mostrar como estas duas novidades trazem consigo, necessariamente, a constituição de uma combinatória. Logo que o sujeito ingressa no caminho de uma dissociação de fatores, ele se encontra diante de novas possibilidades. Em uma situação experimental realizada, o sujeito deveria descobrir se a flexibilidade de uma haste de metal depende do material que é
feita, de seu comprimento, de sua grossura ou de sua forma de corte. Inhelder e Piaget, ao analisar os resultados, apontam que:
(...) de início [o sujeito] associa todos esses fatores entre si por comparação 2
por 2, 3 por 3, etc.; mas isso não ultrapassa as operações multiplicativas do nível concreto (tabelas com 2, 3, ...entradas) e verificamos que essas associações ou correspondências multiplicativas continuam insuficientes para
solução dos problemas, ainda que seja necessário começar pelo seu estabelecimento. Apenas depois, quando essas associações de base já foram construídas, é que entre as combinações possíveis devem ser escolhidas as
combinações que permitem uma comprovação. Portanto, é aqui que aparece necessariamente a combinatória. (INHELDER; PIAGET, 1955, p. 215).
Inhelder e Piaget afirmam que se pode pensar que desses fatores associados cada um atue separadamente, enquanto os outros são conservados invariáveis, e a combinação comprobatória é aquela que faz variar apenas um fator. No entanto, também é possível pensar que dois ou três deles devam intervir simultaneamente para provocar o efeito observado. Também pode ocorrer que haja intervenção de um ou outro, mas cada um com exclusão do outro, ou um em sentido inverso ao do outro. Portanto, é evidente que a dissociação dos fatores chega, segundo o caso, a um certo número de possibilidades distintas que se traduzem por implicações,
equivalências, disjunções, conjunções, exclusões, incompatibilidades, etc. (...).
Numa palavra, a dissociação dos fatores chega necessariamente a combinar entre si, n por n, as associações de base, e, portanto, a substituir as simples operações de multiplicação ou de correspondência, que criaram essas
associações de base, pela combinatória característica do “conjunto das partes”. (INHELDER; PIAGET, 1955, p. 215-216).
Inhelder e Piaget (1955, p. 216), após verificar que a dissociação dos fatores, que ocorre pela necessidade de coordenar entre si os resultados mais complexos das
operações concretas de estabelecimento de relações e correspondências, leva necessariamente a uma combinatória, assinalam que é necessário mostrar como esta
combinatória engendra o pensamento formal. Inhelder e Piaget destacam que é necessário saber de que forma a coordenação das operações concretas chega à combinatória inerente à lógica das proposições e, portanto, ao pensamento formal.
Uma vez que o sujeito classifica, seria, iguala, coloca em correspondência, etc., os diversos aspectos da situação que condicionam a solução de um problema, para resolver o problema pode ser necessário reunir num único sistema as operações até então realizadas, e é a isso que conduz a necessidade de coordenar entre si seus resultados, quando são insuficientemente coerentes. Ora, não há operações que permitam ligar diretamente os diversos agrupamentos de classes e relações num único sistema, sem sair de inclusões
simples, aditivas ou multiplicativas, e, portanto, sem construir seu “conjunto das partes”, isto é, justamente essa combinatória cuja formação no pensamento espontâneo dos sujeitos precisamos agora compreender. (INHELDER; PIAGET,
1955, p. 216).
Inhelder e Piaget informam que, seja para as classes ou para as relações (mas não para as duas coisas ao mesmo tempo), há um agrupamento mais geral que os outros, no sentido que os contém ou em que tais agrupamentos dele derivam por
especificações sucessivas. O agrupamento concreto mais geral é o agrupamento multiplicativo (de classes ou relações) que consiste de tabelas de dupla entrada (ou tripla, etc.). Nesta forma de agrupar os dados, para dois acontecimentos ou
propriedades (x e y), o sujeito constrói associações elementares xy + x y + x y + x y . Assim, novos problemas se apresentam para o sujeito, que precisa decidir quais, entre
essas associações são verdadeiras, e qual é a significação que deve ser atribuída a esses subconjuntos.
É muito interessante verificar que a escolha ou essa verificação dos
subconjuntos de associações verdadeiras, entre as possibilidades xy + x y + x
y + x y , se devem a simples operações de classificação, mas aplicadas às
associações (xy, etc.) e generalizadas a todos os casos possíveis: o sujeito
reúne assim os casos xy aos casos x y , ou o caso xy ao caso x y , etc., como
se se tratasse de uma reunião de objetos qualificados por suas propriedades
comuns, quando, na realidade, se trata de reunir as associações, isto é, as
situações nas quais duas propriedades se apresentam juntas (ou uma sem a
outra, etc.) ou ainda, onde dois acontecimentos se produzem ao mesmo tempo
(ou um sem o outro, etc.). Em outros termos, o sujeito, partindo do conjunto
multiplicativo xy + x y + x y + x y , constrói seu “conjunto de partes” através de
uma nova classificação: portanto, aplica o mais simples dos agrupamentos (a
classificação) ao mais geral (a tabela das multiplicações lógicas), chegando
assim a uma espécie de agrupamento de segunda potência que coordenará
todos os agrupamentos num sistema superior, uma vez que não pode ligá-los
diretamente entre si. (INHELDER; PIAGET, 1955, p. 216-217).
Inhelder e Piaget assinalam que esse agrupamento de segunda potência, por aplicação da classificação generalizada às associações multiplicativas, não é mais do que uma combinatória n por n, e podem-se extrair as seguintes conseqüências quanto à elaboração do pensamento formal:
Em primeiro lugar, essa classificação generalizada das associações xy, etc., chega a um novo modo de composição. Inhelder e Piaget (1955, p. 217) destacam que as classificações anteriormente utilizadas pelo sujeito eram essencialmente formas de inclusão simples (por exemplo, rouxinol < pássaro < animal < ser vivo), de acordo com
o mais elementar dos agrupamentos: A + A‟ = B; B + B‟ = C; etc., ou ainda, as classificações segundo dois critérios possíveis (os genebrinos mais os outros suíços =
os valdenses mais os outros suíços), ou seja, A1 + A‟1 = A2 + A‟2, etc. (vicariância).
Quando se trata de uns nos outros os subconjuntos de associações num agrupamento multiplicativo, levando em consideração as diferentes possibilidades, o modo de
composição será muito diverso e chegará a uma combinação n por n por generalização da vicariância.
Por exemplo, dado os elementos x e y, as quatro associações possíveis podem ser representadas pelos números de 1 a 4:
_ _ ___
1 = xy; 2 = x y ; 3 = x y e 4 = x y
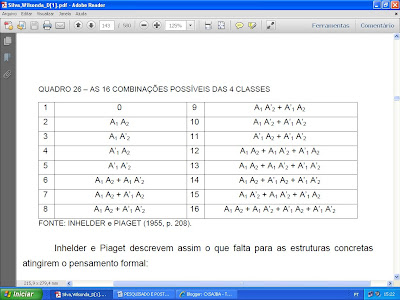
As classes resultantes das inclusões possíveis serão 16 (veja o quadro 26):
(0)
(1); (2); (3); (4)
(1 + 2); (1 + 3); (1 + 4); (2 + 3); (2 + 4); (3 + 4)
(1 + 2 + 3); (1 + 2 + 4); (1 + 3 + 4); (2 + 3 + 4)
(1 + 2 + 3 + 4)
Essas classes, cuja construção se efetua pouco a pouco na mente do sujeito,
seja pela verificação das situações reais, seja pela dedução das combinações
possíveis, apresentam uma estrutura nova se comparada à dos agrupamentos das
operações concretas. Em outras palavras:
(...) o sistema novo que se constitui assim não é mais uma classificação simples
(nem mesmo uma vicariância entre classes das mesmas séries): é uma
classificação generalizada ou conjunto de todas as classificações possíveis
compatíveis com as associações de base que são dadas. (INHELDER;
PIAGET, 1955, p. 218).
Assim, a negação de uma combinação qualquer (por exemplo, da conjunção xy,
associação 1) não precisa mais ser construída por aproximações sucessivas por
classes complementares sob as classes mais amplas e mais próximas, como ocorre
nos agrupamentos concretos (se A é a classe dos pardais e B a dos pássaros, a
complementar escolhida pelo sujeito para A não é a negação absoluta Ā, isto é, o
conjunto das realidades que não são os pardais, mas A’, isto é, os pássaros que não
são os pardais; e se C é a classe dos animais, B‟ será a dos animais que não são
pássaros, etc.): a negação de uma combinação será o conjunto das outras, isto é, sua
complementar dentro do todo: a conjunção x ∙ y (associação 1) terá como negação x y
+ x y + x y (associação 2 + 3 + 4), ou seja, a incompatibilidade (x/y). (INHELDER;
PIAGET, 1955, p. 218).
Dessa forma, o sistema assim construído comporta ao mesmo tempo as
inversões (ou seja, as negações apresentadas no item anterior) e as reciprocidades (x
y e y x, etc.), e essas inversões e reciprocidades constituem um grupo de quatro
transformações, sendo que o sujeito não toma consciência desse grupo sob sua forma mais geral, mas que apresenta repercussões no pensamento do sujeito. (INHELDER;
PIAGET, 1955, p. 218).
_
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
4.4 A INTELIGÊNCIA OPERATÓRIA FORMAL
Para Inhelder e Piaget (1955, p. 183-184), o estudo do desenvolvimento psicológico do pensamento pode ser feito em dois pontos de vista complementares: o das condições de equilíbrio e o das condições das estruturas. Do ponto de vista das condições de equilibro, o pensamento parece, em cada uma das suas formas, passar de estados menos equilibrados a estados mais equilibrados, sendo possível identificar
dois fatores principais relativos à essa equilibração pior ou melhor: um relativo à
extensão maior ou menor do campo do equilíbrio, e o outro aos instrumentos de
coordenação, ou seja, às estruturas de que a inteligência dispõe nos níveis
considerados.
Do ponto de vista das condições das estruturas, o problema consiste em
verificar a filiação das estruturas que caracterizam essas coordenações, assim como
seu modo de construção. Essa construção depende de três fatores principais: a
maturação do sistema nervoso, a experiência adquirida em função do meio físico, e a
ação do meio social. No entanto, Piaget destaca que estes fatores só atuam, respectiva
e concorrentemente, ao se submeterem às leis de equilíbrio que determinam as
melhores formas de adaptação compatíveis com o conjunto das condições em jogo.
“Portanto, o equilíbrio e a estrutura são os dois aspectos complementares de toda
organização do pensamento.” (INHELDER; PIAGET, 1955, p. 184).
4.4.1 O pensamento formal do ponto de vista do equilíbrio
Inhelder e Piaget (1955, p. 185) destacam que a principal característica do
pensamento formal está ligada ao papel que dá ao possível com relação às verificações
de realidade, e que comparado ao pensamento concreto, constitui uma nova forma de
equilíbrio.
Ao final do período sensório-motor, por intermédio da função simbólica, uma
nova forma de pensamento se desenvolve na criança. Esta forma de pensamento é de
natureza pré-lógica (ou pré-operatória) e difere do pensamento operatório concreto sob
três aspectos: primeiro, ao considerar situações estáticas, a criança tende a explicá-las
em função de seus caracteres de configuração atual, mais do que em função das
transformações que levam de uma situação a outra. Segundo, o pensamento do sujeito,
no que se refere a essas transformações, assimila-as às ações pessoais do sujeito e
não a operações reversíveis. Estas duas diferenças podem ser reduzidas a uma: os
estados e as modificações ainda não formam, no nível do pensamento intuitivo, um sistema único, enquanto que no nível das operações concretas as situações se
subordinarão às transformações em si mesmas. Terceiro, já existe neste nível uma
tendência para a formação de sistemas de conjunto, mas a reversibilidade neste
período é ainda incompleta. (INHELDER; PIAGET, 1955, p. 185-186).
Já com o surgimento do pensamento concreto, o sistema das regulações, até
então sem estabilidade, chega a uma primeira forma de equilíbrio estável:
(...) ao atingir o nível da reversibilidade completa, as operações concretas
decorrentes das regulações precedentes se coordenam, na realidade, em
estruturas definidas (classificações, seriações, correspondências, etc.) que se
conservarão durante toda a vida, sem excluir a formação de sistemas
superiores, mas continuando ativos no plano limitado da organização dos dados
imediatos. (INHELDER; PIAGET, 1955, p. 187).
Esta forma de equilíbrio consiste, em primeiro lugar, em que os domínios
sucessivamente estruturados por esse pensamento concreto não admitem mais
oposição entre as situações estáticas e as transformações, sendo que as primeiras
subordinam-se às segundas, no sentido em que cada estado é concebido como
resultado de uma transformação.
Em segundo lugar, afirmar que o sistema das transformações está em equilíbrio
significa dizer que essas transformações adquiriram uma forma reversível e a
potencialidade para se coordenar segundo as leis fixas da composição, sendo que as
transformações são agora assimiladas às operações.
Em terceiro lugar, o pensamento operatório concreto, comparado ao
pensamento intuitivo pré-operatório, caracteriza-se por uma extensão do real na direção
do virtual, pois classificar objetos significa construir conjuntos de tal forma que novos
objetos possam ser ligados aos objetos já classificados, e novas inclusões se tornem
possíveis. Da mesma forma, seriar objetos em ordem comporta novas subdivisões
possíveis, mas estas possibilidades intrínsecas às operações concretas não estão
ainda abertas para um campo mais ou menos amplo de hipóteses, como será o caso
das operações formais. (INHELDER; PIAGET, 1955, p. 187).
(...) o pensamento concreto continua fundamentalmente ligado ao real, e o
sistema das operações concretas, que constitui a forma final de equilíbrio do
pensamento intuitivo, chega apenas a um conjunto restrito de transformações
virtuais, e, portanto, a uma noção do “possível” que é apenas uma extensão
(não muito grande) do real. Este caráter do pensamento concreto é muito claro
(...) [ao se comparar] o pensamento concreto da criança ao pensamento formal
do pré-adolescente ou do adolescente; enquanto que estes últimos, para
resolver o problema que lhes é proposto, começam imediatamente a construir
um conjunto de hipóteses entre as quais precisarão escolher
experimentalmente a melhor, a criança do nível concreto a rigor não cria
hipóteses. Age desde o começo, e apenas procura, durante sua ação,
coordenar as leituras sucessivas dos resultados que obtém, o que significa
estruturar a realidade na qual atua. Ou, se admitimos que cria hipóteses, é
preciso esclarecer que estas são apenas projetos de ações possíveis, e não,
como no adolescente, formas de imaginar o que deveria ser o real se tal ou qual
condição hipotética fosse satisfeita. (INHELDER; PIAGET, 1955, p. 188).
Inhelder e Piaget (1955, p. 189-191) apontam quatro características do
pensamento formal: inversão de sentido entre o real e o possível, o que faz com que o
pensamento formal seja essencialmente hipotético-dedutivo. O pensamento formal
refere-se a elementos verbais, e não mais diretamente aos objetos. O pensamento
formal constitui um sistema de operações de segunda potência. E por último a
utilização de um procedimento combinatório.
Com o pensamento formal ocorre uma inversão de sentido entre o real e o
possível, pois em vez de o possível se manifestar simplesmente sob a forma de um
prolongamento do real ou das ações executadas na realidade, é, ao contrário, o real
que se subordina ao possível. No pensamento formal, os fatos são concebidos como o
setor das realizações efetivas no meio de um universo de transformações possíveis,
pois não são explicados, e nem admitidos como fatos, senão depois de uma verificação
que se refere ao conjunto das hipóteses compatíveis com a situação dada.
É esta inversão de sentido entre o real e o possível que, mais que qualquer
outra propriedade subseqüente, caracteriza o pensamento formal: em vez de
apenas introduzir um início de necessidade no real, como ocorre nas
inferências concretas, realiza desde o início a síntese entre o possível e o
necessário, deduzindo com rigor as conclusões de premissas, cuja verdade
inicialmente é admitida apenas por hipótese, e, assim, vai do possível para o real. (INHELDER; PIAGET, 1955, p. 189).
Dessa forma, o pensamento formal é essencialmente hipotético-dedutivo, sendo
que a dedução não mais se refere a realidades percebidas, mas a enunciados
hipotéticos, isto é, a proposições que se referem a hipóteses ou apresentam dados
apenas como simples dados, independente do seu caráter real. Assim, a dedução
consiste em ligar estas suposições, e delas deduzir suas conseqüências necessárias,
mesmo quando sua verdade experimental não ultrapassa o possível. (INHELDER;
PIAGET, 1955, p. 189).
O pensamento formal também possui a propriedade de referir-se a elementos
verbais, e não mais diretamente aos objetos, embora nem todo pensamento verbal seja
formal. Quando os objetos são substituídos por enunciados verbais, superpõe-se uma
nova lógica – a das proposições – à das classes e relações que se referem a esses
objetos, e esta é uma segunda propriedade fundamental do pensamento formal. E esta
lógica das proposições comporta um número bem maior de possibilidades operatórias
do que os simples agrupamentos de classes e de relações. Assim, é o número de
operações possíveis que, inicialmente, a distingue funcionalmente do pensamento
concreto, pois, a prova disso é que a lógica das proposições se manifesta sob suas
formas mais características, tanto diante de situações experimentais, como diante de
problemas puramente verbais. (INHELDER; PIAGET, 1955, p. 190).
Inhelder e Piaget (1955, p. 190) destacam que o papel do pensamento formal
não se reduz a traduzir em palavras ou em proposições o que poderia ter sido
executado concretamente sem o seu recurso. Ao contrário, é durante as manipulações
experimentais que se afirma, no início do pensamento formal, uma série de
possibilidades operatórias novas, formadas por disjunções, implicações, exclusões, etc.,
que intervêm desde a organização da experiência e desde a leitura dos dados de fato.
A razão disso é que desde o contato com os problemas de fato, o pensamento formal
parte da hipótese, ou seja, do possível, em vez de limitar-se a uma estruturação direta
dos dados percebidos.
Assim, o característico da lógica das proposições não é ser uma lógica verbal.
É, antes de tudo, uma lógica de todas as combinações possíveis do pensamento, tanto
no caso em que tais combinações aparecem com problemas experimentais, quanto no caso em que aparecem diante de problemas puramente verbais.
E o motor efetivo da lógica das proposições é o poder de combinar, graças ao
qual ela insere o real no conjunto das hipóteses possíveis, compatíveis com os dados.
Inhelder e Piaget (1955, p. 190-191) destacam ainda que o pensamento formal
se constitui num sistema de operações de segunda potência. As operações concretas
são as operações de primeira potência, pois se referem diretamente aos objetos, como
por exemplo, a construção de relações entre elementos dados. No entanto, também é
possível construir relações entre relações, como por exemplo, as proporções, cuja
conquista só é obtida no nível formal, sendo que as proporções supõe as operações de
segunda potência.
Esta noção de operação de segunda potência exprime novamente o caráter
geral do pensamento formal, que é o de ultrapassar o quadro das
transformações que se referem diretamente ao real (operações de primeira
potência) subordinando-as a um sistema de combinações hipotético-dedutivas,
e, portanto, simplesmente possíveis. (INHELDER; PIAGET, 1955, p. 191).
Por fim, Inhelder e Piaget destacam o caráter combinatório do pensamento
formal, pois para lidar com o possível, o sujeito precisa de um instrumento para gerá-lo,
e esse instrumento é uma combinatória, um procedimento para combinar elementos
que, diante de uma situação determinada, permite ao sujeito a produção de todos os
casos possíveis. Inhelder e Piaget afirmam que “apenas uma combinação dá o conjunto
dos possíveis e, no terreno experimental, a pesquisa das combinações novas é
precisamente o que caracteriza a hipótese.” (1955, p. 191). Ver quadro 24.
QUADRO 24 – CARACTERÍSTICAS DO PENSAMENTO FORMAL.
Do ponto de vista físico, sabe-se que um estado de equilíbrio se caracteriza pela compensação entre todas as modificações virtuais, compatíveis com as ligações
do sistema considerado. No dizer de Inhelder e Piaget (1955, p. 193):
(...) para conceber o possível, o pensamento formal é obrigado a dispor, em cada situação específica, de uma grande amplitude de operações virtuais que ultrapassam o domínio das operações momentaneamente utilizadas de fato, e
tais operações virtuais constituem uma condição necessária de equilíbrio, e isso, pelas duas razões seguintes: de um lado, são elas que correspondem ao que na linguagem da teoria do equilíbrio, denominamos as “transformações virtuais”; de outro, há equilíbrio na medida em que essas transformações virtuais “se
compensam” exatamente, ou, na linguagem das operações, na medida em que tais operações possíveis constituem um sistema rigorosamente reversível do
ponto de vista lógico.
Do ponto de vista lógico, a significação lógica representa um caráter indispensável para o funcionamento do pensamento hipotético-dedutivo ou formal.
Deve-se ter em mente que, na realidade, o possível formal é o correlato obrigatório, de noção e de necessidade.
Inhelder e Piaget (1955, p. 193) destacam que:
Uma afirmação relativa apenas ao real – por exemplo, um juízo de existência ou um juízo predicativo – não precisa ser necessário: a afirmação é verdadeira ou falsa, na medida em que corresponde ou não a um fato. Uma dedução que refere a uma hipótese (ou a um dado de fato, mas admitido como hipótese), é, ao contrário, necessariamente verdadeira, do ponto de vista formal, desde que seja correta, e isso independentemente do valor da hipótese admitida. A
conexão marcada pelas palavras “se...então” (implicação inferencial) consiste em ligar uma conseqüência necessária a uma afirmação simplesmente possível: é esta síntese do necessário e do possível que caracteriza o emprego desse possível no pensamento formal, por oposição ao possível extensão-doreal do pensamento concreto e às possibilidades não reguladas, características das ficções da imaginação.
Inhelder e Piaget (1955, p. 193-194), ao indagar em que consiste este possível formal, argumentam “é possível tudo que não é contraditório”. Assim, a reversibilidade operatória formal que, na perspectiva física significa a exata compreensão das transformações (ou operações) virtuais, adquire na perspectiva lógica, a significação da
necessidade dedutiva.
No conjunto, esses dois aspectos, físico e lógico, da noção de possível,
psicologicamente constituem apenas um: ao situar um estado real num sistema
de transformações possíveis, o pensamento formal assegura, simultaneamente,
seu equilíbrio, do ponto de vista da conservação psicológico ulterior das
estruturas que desenvolve, e seu valor de instrumento lógico necessário, do
ponto de vista da utilização dessas estruturas, enquanto instrumentos
dedutivos. (INHELDER; PIAGET, 1955, p. 194).
Inhelder e Piaget (1955, p. 195) apontam duas significações psicológicas para a
palavra possível: o materialmente possível e o estruturalmente possível. O
materialmente possível é o possível do ponto de vista do sujeito, e refere-se às
operações ou relações que o sujeito concebe como possível, ou seja, aquilo que o
sujeito sabe que pode efetuar ou construir, mesmo que não o faça efetivamente. O
estruturalmente possível é o possível do ponto de vista do observador, e são as
operações e relações que o sujeito seria capaz de efetuar ou de construir, mas sem que
pense fazê-lo, ou seja, sem que tome consciência dessa eventualidade, nem de sua
capacidade a respeito. Inhelder e Piaget (1955, p. 196) destacam que:
(...) sempre devem ser consideradas, num ato de inteligência, as operações
reais, no sentido de efetivamente realizadas no pensamento consciente do
sujeito, e as operações “estruturalmente possíveis”, isto é, que não efetua, mas
que poderia efetuar. (...) é esse possível relativo às estruturas operatórias, de
que o sujeito dispõe, que constitui o possível do ponto de vista do observador e
que, portanto, corresponde, no domínio físico, às transformações virtuais, não
efetivamente realizadas.
O materialmente possível tem estreitas relações com o estruturalmente
possível, do qual constitui um primeiro plano de atualização: é na medida em que o
sujeito dispõe de um número suficiente de operações estruturalmente possíveis que
chega a imaginar as transformações materialmente possíveis. No dizer de Inhelder e
Piaget:
Sem um certo jogo de possibilidades estruturais (e é o que se manifesta
claramente ao nível pré-operatório, e mesmo no das operações concretas), não
poderia verificar os estados de fatos percebidos no real, os estados estáticos ou
as transformações atuais, e não chegaria a ter uma representação das
transformações hipotéticas que servem para que imagine novas experiências.
Portanto, o materialmente possível depende do estruturalmente possível.
(INHELDER; PIAGET, 1955, p. 196).
114
4.4.2 O pensamento formal do ponto de vista das Estruturas
Depois de caracterizar a diferença entre o pensamento concreto e pensamento
formal do ponto de vista do equilíbrio, por intermédio da extensão progressiva do
conjunto das operações virtuais ou possíveis, Inhelder e Piaget destacam que é
necessário comparar as estruturas totais que correspondem a essas duas formas de
equilíbrio.
Inhelder e Piaget (1955, p. 205) afirmam que todo estado de equilíbrio pode ser
reconhecido por uma certa forma de reversibilidade. Do ponto de vista estrutural, a
reversibilidade, que é a possibilidade permanente de uma volta ao ponto de partida, se
apresenta sob duas formas distintas e complementares. Pode-se voltar ao ponto de
partida anulando-se a operação efetuada, o que constitui uma inversão ou negação: o
produto da operação direta e de seu inverso é a operação nula ou idêntica. Mas
também se pode voltar ao ponto de partida anulando uma diferença (no sentido lógico
do termo), o que constitui uma reciprocidade: o produto de duas operações recíprocas
é, não uma operação nula, mas uma equivalência.
A inversão e a reciprocidade são encontradas sob aspectos diferentes em todos
os estádios de desenvolvimento, pois constituem as condições de equilíbrio das
ações mais elementares, bem como das ações superiores. É assim que no nível
perceptivo (embora não exista ainda nenhuma reversibilidade completa) as
inversões correspondem às adjunções ou supressões de elementos e as
reciprocidades às simetrias ou semelhanças. (INHELDER; PIAGET, 1955, p.
205).
Existe uma primeira diferença importante entre as estruturas concretas e
formais: enquanto que as segundas chegam a reunir as inversões e as reciprocidades
em um sistema único de transformações (o grupo INRC), os sistemas característicos
das operações concretas, ou agrupamentos de classes e de relações, decorrem da
inversão (classes) ou da reciprocidade (relações), sem síntese geral dessas duas
formas de reversibilidade. (INHELDER; PIAGET, 1955, p. 205-206).
115
De uma maneira geral, os “agrupamentos” elementares, que constituem as
únicas estruturas de conjunto acessíveis ao nível das operações concretas, se
caracterizam, portanto, por duas particularidades essenciais que as opõe às
estruturas formais: 1) Constituem sistemas de inclusões ou de encadeamentos
simples ou múltiplos, mas sem combinatória que inclua uma combinatória que
ligue os diversos elementos de n por n; por conseguinte não atingem a estrutura
do reticulado que comporta uma tal combinatória (“conjunto das partes”), mas
permanecem no estado de semi-reticulados; 2) Apresentam uma reversibilidade
que consiste seja em inversão (classes), seja em reciprocidade (relações), mas
não chegam a reunir essas duas formas de reversibilidade num sistema único;
por isso, não coincidem com a estrutura do grupo das inversões e
reciprocidades (o grupo INRC) e permanecem no estado de grupos
incompletos. (INHELDER; PIAGET, 1955, p. 207).
As estruturas concretas de classes consistem exclusivamente de classificações
simples (aditivas) ou multiplicativas (tabelas multiplicativas ou matrizes), de tal forma
que cada classe depende daquelas de que faz parte (A incluído em B, B em C, etc.) e
se opõe à sua complementar com relação à classe imediatamente superior (A‟ = B – A :
B‟ = C – B; etc.), mas sem combinatória que dê todos os sub-conjuntos possíveis de
classes no interior do sistema. Essas estruturas repousam exclusivamente na
reversibilidade por inversão: o sujeito pode assim reunir duas classes contíguas numa
única classe (A + A‟ = B; etc.) ou subtrair uma do todo assim formado (A = B – A‟); pode
também multiplicar uma classe pela outra (A1 x A2 = A1A2) ou abstrair uma do todo
assim formado (A1A2 : A2 = A1); mas tais sistemas ignoram a forma geral da
reciprocidade. (INHELDER; PIAGET, 1955, p. 206).
Inhelder e Piaget afirmam que as estruturas concretas de relações coordenam
entre si as equivalências completas (igualdades) ou parciais (alteridades) no caso de
relações simétricas, as diferenças ordenadas no caso das relações assimétricas
transitivas (seriações ou encadeamentos) e comportam igualmente os sistemas
multiplicativos (correspondências, etc.). A reversibilidade característica dessas
estruturas consiste de reciprocidades.
Para se entender a capacidade da inteligência operatória formal convém
compará-la com os agrupamentos mais complexos de que a inteligência operatória
concreta é capaz: as classificações multiplicativas (matrizes). Piaget e Inhelder (1959,
p. 188) fornecem o exemplo: dado um jogo de elementos de duplas características
(quadrados e círculos, vermelhos e azuis) que podem ser repartidos em duas classes
116
A1 e A‟1, segundo uma das suas características (A1= quadrados e A‟1= círculos) e,
igualmente, em duas classes A2 e A‟2, segundo a outra característica (A2= vermelhos e
A‟2= azuis), chama-se B1 à reunião das duas primeiras classes (formas), ou seja, B1= A1
+ A‟1, e B2 à reunião das duas segundas (cores), ou seja, B2= A2 + A‟2.
A classificação multiplicativa consiste em classificar esses elementos ao mesmo
tempo, segundo a classificação aditiva B1 e segundo a classificação aditiva B2, o que
originará quatro classes distintas: A1 A2+ A1 A‟2 + A‟1 A2 + A‟1 A‟2. Para resolver o
problema o sujeito deve, necessariamente, construir uma matriz de duas dimensões
(quadro de dupla entrada m n), como pode ser visto a seguir:
QUADRO 25 – MATRIZ DE DUPLA ENTRADA.
(...) o que falta às estruturas concretas de agrupamento é a combinatória intrínseca à construção do “conjunto das partes”, ou, o que é a mesma coisa, é a utilização de operações proposicionais (implicação, etc.) ou isomórficas
destas últimas, pois as operações interproposicionais repousam sobre a estrutura desse “conjunto das partes”. A diferença entre os agrupamentos elementares de classes e de relações (classificações, seriações e correspondências multiplicativas) e esta estrutura é que os primeiros constituem somente remi-reticulados, enquanto que o conjunto das partes forma um reticulado completo. Em segundo lugar, as operações com o “conjunto das partes” comportam uma inversa e uma recíproca: a segunda diferença essencial
entre os agrupamentos concretos e o sistema de operações formais refere-se, então, à ausência de um grupo único que ligue as inversões e reciprocidades nos agrupamentos elementares, bem como a presença desse grupo logo que se constitui o “conjunto das partes”. (INHELDER; PIAGET, 1955, p. 207).
Inhelder e Piaget destacam que não é suficiente assinalar estas diferenças entre as operações concretas e formais, mas de compreender o que leva o sujeito, por volta de 11 ou 12 anos, a construir efetivamente os “conjuntos das partes”. Com o objetivo de identificar em que casos os sujeitos utilizavam ou não as operações proposicionais, Inhelder e Piaget afirmam que “é quase impossível, diante de um
enunciado isolado qualquer, decidir entre essas duas possibilidades, e a questão não apresenta significação psicológica a não ser em função do conjunto dos raciocínios do sujeito ou de uma seqüência suficientemente sistemáticas de inferências.” Portanto, a linguagem dos sujeitos não traduz, senão de uma maneira muito aproximada, a estrutura real de seus pensamentos. (INHELDER; PIAGET, 1955, p. 209-210).
Inhelder e Piaget (1955, p. 210) propõem que é mais adequado comparar todos os enunciados, e, sobretudo todas as ações de um mesmo sujeito. Assim, pode-se ver se o sujeito se limita a uma simples leitura dos resultados brutos da experiência para destes extrair apenas classificações, seriações ou correspondências, ou se tenta dissociar os fatores, o que implica, ao mesmo tempo, um raciocínio hipotético-dedutivo
e uma combinatória.
Inhelder e Piaget destacam que a passagem das operações concretas para as operações formais não ocorre por um salto brusco, mas sim por múltiplas transições que o sujeito vai passar desde o nível da simples leitura dos fatos brutos, por meio de classificações, seriações e correspondências, para o nível da combinatória. Ao indagar sobre por que o equilíbrio final das operações combinatórias é tão
tardio, Inhelder e Piaget afirmam que:
(...) na medida em que as operações derivam umas das outras por coordenações progressivas, e em que as mais simples procedem da ação irreversível, compreendemos as razões pelas quais o equilíbrio das operações
combinatórias é tão tardio: o sujeito deve, inicialmente, dessubjetivar suas
ações para torná-las reversíveis, o que equivale a coordená-las em agrupamentos elementares ainda próximos da manipulação, e depois, como não consegue imediatamente dissociar inteiramente a forma e o conteúdo, é obrigado a reconstruir esses diversos agrupamentos nos domínios heterogêneos sucessivos que lhe impõe a experiência; é somente depois dessa estruturação progressiva dos diferentes conteúdos da experiência que um mecanismo formal geral começa a ser isolado por coordenação de conjunto. (INHELDER; PIAGET, 1955, p. 211).
Inhelder e Piaget destacam que enquanto as operações concretas procedem conteúdo por conteúdo, a realidade cedo ou tarde impõe uma mistura de conteúdos, forjando novos instrumentos operatórios. Dois métodos são então empregados pelo sujeito: no primeiro, o sujeito procura coordenar entre si os resultados das operações concretas, ou seja, eliminar as contradições aparentes; no segundo, o sujeito procura
coordenar diretamente entre si as diversas operações características dos agrupamentos concretos. Inhelder e Piaget assinalam que esses dois métodos conduzem à
descoberta da lógica formal das proposições, que consistem em: 1) Dissociar os conteúdos estruturados apenas pelas operações concretas, de maneira a coordenar os resultados dessas operações, em função das diversas combinações possíveis; 2) Coordenar os diversos agrupamentos de classes e de relações num único sistema total. Esses dois processos, por mais diferentes que possam parecer entre si, na realidade se reduzem a um só, pois os dois repousam numa combinatória. (INHELDER; PIAGET, 1955, p. 212).
No nível das operações concretas o sujeito procura estruturar a realidade de maneira mais completa que lhe é acessível, mas se limita ao real sob sua forma bruta.
A razão para isso é que as operações concretas (entre os 7 e 12 anos) têm por função estruturar o real, domínio por domínio, considerando esses conteúdos um após o outro,
às vezes com intervalo de alguns anos entre eles, como no caso das decalagens.
(...) quanto mais o sujeito analisa concretamente (portanto por simples correspondências entre os conteúdos distintos) a realidade, mais esta lhe apresenta misturas de regularidades parciais e exceções, e que não podem ser interpretadas com segurança. Inicialmente, é natural que o sujeito despreze,
seja as regularidades parciais, seja, principalmente, as exceções; mas, quando começa a levar a sério as exigências da experiência, encontra-se diante de uma situação sem saída do ponto de vista da simples descrição concreta dos fatos
brutos. (INHELDER; PIAGET, 1955, p. 213).
Inhelder e Piaget destacam que, cedo ou tarde, se impõe uma nova atitude experimental, que se pronuncia em numerosos casos desde o nível concreto, mas não
se generaliza antes do nível formal: é a tentativa de dissociar os fatores. Para compreender em que consiste essa tentativa de dissociar os fatores, deve-se analisar:
sob que formas nasce essa tentativa; sob que formas se generaliza e porque se generaliza tardiamente; como conduz necessariamente a uma combinatória. (INHELDER; PIAGET, 1955, p. 213).
No nível concreto, já existem algumas formas de dissociação de fatores, pois, tratando de decidir se determinado fator desempenha um papel ou não no resultado dado, o sujeito desse nível já é capaz de alguns processos, alguns por observação pura, outros por experimentação. Inhelder e Piaget informam que nesses dois casos (observação ou experimentação), a dissociação dos fatores, característica do nível concreto, é uma dissociação por negação, ou seja, o fator cujo papel é discutido às vezes está presente, às vezes ausente (observação) ou então é introduzido ou afastado
(experimentação). Portanto, tem-se aí exclusivamente transformações por inversão ou negação, e não reciprocidades; assim, tem-se a primeira e não as duas formas de reversibilidade.
Uma segunda diferença entre as dissociações elementares do nível das operações concretas e a dissociação do nível das operações formais é que, no caso de
dois ou vários fatores, x, y, etc., o sujeito não introduz e nem elimina o fator x a não ser para ver se desempenha sozinho um papel ativo, e não para estudar as variações de y.
Os sujeitos do nível formal, ao contrário, afastarão um fator x, e não somente para controlar sua influência, mas também para analisar a de y, sem perturbação por parte
de x. (INHELDER; PIAGET, 1955, p. 213-214).
As duas descobertas características do início do nível formal são que o sujeito pode dissociar fatores por neutralização, assim como por exclusão, e que é necessário
afastar um fator, não somente para analisar sua ação, mas ainda para mostrar a de outros fatores presentes. No dizer de Inhelder e Piaget:
É então que aparece a conduta característica do nível III [formal], que consiste em, diante de associações x, y, afastar y para estudar x sem interferências
perturbadoras, e reciprocamente. Portanto, a necessidade de excluir um fator para fazer variar um outro nasce de uma inversão de sentido na construção de correspondências, tendendo a abstrair ou a dissociar, em vez de multiplicar ou
associar, e isso diante da excessiva complexidade e das contradições que caracterizam a experiência bruta. Diante disso, alguns fatores podem ser afastados por inversão ou negação, mas isso não ocorre com todos. A segunda novidade característica do estádio III consiste em generalizar esta exclusão dos fatores perturbadores no caso em que tais fatores não comportam negação: neste caso o que é negado não é mais um dos termos (propriedade ou acontecimento), mas a diferença entre eles. Em outras palavras, o fator que
deve ser excluído é simplesmente neutralizado por igualização dos termos existentes, o que constitui uma reciprocidade, e não mais uma inversão. (INHELDER; PIAGET, 1955, p. 214-215).
Inhelder e Piaget afirmam que a dissociação de fatores, característica do nível formal, introduz uma reversibilidade por reciprocidade, ao mesmo tempo que por inversão, ao utilizar, de maneira paralela, as duas formas de reversibilidade, e ao tornálas funcionalmente equivalentes.
Inhelder e Piaget destacam que ainda é necessário mostrar como estas duas novidades trazem consigo, necessariamente, a constituição de uma combinatória. Logo que o sujeito ingressa no caminho de uma dissociação de fatores, ele se encontra diante de novas possibilidades. Em uma situação experimental realizada, o sujeito deveria descobrir se a flexibilidade de uma haste de metal depende do material que é
feita, de seu comprimento, de sua grossura ou de sua forma de corte. Inhelder e Piaget, ao analisar os resultados, apontam que:
(...) de início [o sujeito] associa todos esses fatores entre si por comparação 2
por 2, 3 por 3, etc.; mas isso não ultrapassa as operações multiplicativas do nível concreto (tabelas com 2, 3, ...entradas) e verificamos que essas associações ou correspondências multiplicativas continuam insuficientes para
solução dos problemas, ainda que seja necessário começar pelo seu estabelecimento. Apenas depois, quando essas associações de base já foram construídas, é que entre as combinações possíveis devem ser escolhidas as
combinações que permitem uma comprovação. Portanto, é aqui que aparece necessariamente a combinatória. (INHELDER; PIAGET, 1955, p. 215).
Inhelder e Piaget afirmam que se pode pensar que desses fatores associados cada um atue separadamente, enquanto os outros são conservados invariáveis, e a combinação comprobatória é aquela que faz variar apenas um fator. No entanto, também é possível pensar que dois ou três deles devam intervir simultaneamente para provocar o efeito observado. Também pode ocorrer que haja intervenção de um ou outro, mas cada um com exclusão do outro, ou um em sentido inverso ao do outro. Portanto, é evidente que a dissociação dos fatores chega, segundo o caso, a um certo número de possibilidades distintas que se traduzem por implicações,
equivalências, disjunções, conjunções, exclusões, incompatibilidades, etc. (...).
Numa palavra, a dissociação dos fatores chega necessariamente a combinar entre si, n por n, as associações de base, e, portanto, a substituir as simples operações de multiplicação ou de correspondência, que criaram essas
associações de base, pela combinatória característica do “conjunto das partes”. (INHELDER; PIAGET, 1955, p. 215-216).
Inhelder e Piaget (1955, p. 216), após verificar que a dissociação dos fatores, que ocorre pela necessidade de coordenar entre si os resultados mais complexos das
operações concretas de estabelecimento de relações e correspondências, leva necessariamente a uma combinatória, assinalam que é necessário mostrar como esta
combinatória engendra o pensamento formal. Inhelder e Piaget destacam que é necessário saber de que forma a coordenação das operações concretas chega à combinatória inerente à lógica das proposições e, portanto, ao pensamento formal.
Uma vez que o sujeito classifica, seria, iguala, coloca em correspondência, etc., os diversos aspectos da situação que condicionam a solução de um problema, para resolver o problema pode ser necessário reunir num único sistema as operações até então realizadas, e é a isso que conduz a necessidade de coordenar entre si seus resultados, quando são insuficientemente coerentes. Ora, não há operações que permitam ligar diretamente os diversos agrupamentos de classes e relações num único sistema, sem sair de inclusões
simples, aditivas ou multiplicativas, e, portanto, sem construir seu “conjunto das partes”, isto é, justamente essa combinatória cuja formação no pensamento espontâneo dos sujeitos precisamos agora compreender. (INHELDER; PIAGET,
1955, p. 216).
Inhelder e Piaget informam que, seja para as classes ou para as relações (mas não para as duas coisas ao mesmo tempo), há um agrupamento mais geral que os outros, no sentido que os contém ou em que tais agrupamentos dele derivam por
especificações sucessivas. O agrupamento concreto mais geral é o agrupamento multiplicativo (de classes ou relações) que consiste de tabelas de dupla entrada (ou tripla, etc.). Nesta forma de agrupar os dados, para dois acontecimentos ou
propriedades (x e y), o sujeito constrói associações elementares xy + x y + x y + x y . Assim, novos problemas se apresentam para o sujeito, que precisa decidir quais, entre
essas associações são verdadeiras, e qual é a significação que deve ser atribuída a esses subconjuntos.
É muito interessante verificar que a escolha ou essa verificação dos
subconjuntos de associações verdadeiras, entre as possibilidades xy + x y + x
y + x y , se devem a simples operações de classificação, mas aplicadas às
associações (xy, etc.) e generalizadas a todos os casos possíveis: o sujeito
reúne assim os casos xy aos casos x y , ou o caso xy ao caso x y , etc., como
se se tratasse de uma reunião de objetos qualificados por suas propriedades
comuns, quando, na realidade, se trata de reunir as associações, isto é, as
situações nas quais duas propriedades se apresentam juntas (ou uma sem a
outra, etc.) ou ainda, onde dois acontecimentos se produzem ao mesmo tempo
(ou um sem o outro, etc.). Em outros termos, o sujeito, partindo do conjunto
multiplicativo xy + x y + x y + x y , constrói seu “conjunto de partes” através de
uma nova classificação: portanto, aplica o mais simples dos agrupamentos (a
classificação) ao mais geral (a tabela das multiplicações lógicas), chegando
assim a uma espécie de agrupamento de segunda potência que coordenará
todos os agrupamentos num sistema superior, uma vez que não pode ligá-los
diretamente entre si. (INHELDER; PIAGET, 1955, p. 216-217).
Inhelder e Piaget assinalam que esse agrupamento de segunda potência, por aplicação da classificação generalizada às associações multiplicativas, não é mais do que uma combinatória n por n, e podem-se extrair as seguintes conseqüências quanto à elaboração do pensamento formal:
Em primeiro lugar, essa classificação generalizada das associações xy, etc., chega a um novo modo de composição. Inhelder e Piaget (1955, p. 217) destacam que as classificações anteriormente utilizadas pelo sujeito eram essencialmente formas de inclusão simples (por exemplo, rouxinol < pássaro < animal < ser vivo), de acordo com
o mais elementar dos agrupamentos: A + A‟ = B; B + B‟ = C; etc., ou ainda, as classificações segundo dois critérios possíveis (os genebrinos mais os outros suíços =
os valdenses mais os outros suíços), ou seja, A1 + A‟1 = A2 + A‟2, etc. (vicariância).
Quando se trata de uns nos outros os subconjuntos de associações num agrupamento multiplicativo, levando em consideração as diferentes possibilidades, o modo de
composição será muito diverso e chegará a uma combinação n por n por generalização da vicariância.
Por exemplo, dado os elementos x e y, as quatro associações possíveis podem ser representadas pelos números de 1 a 4:
_ _ ___
1 = xy; 2 = x y ; 3 = x y e 4 = x y
As classes resultantes das inclusões possíveis serão 16 (veja o quadro 26):
(0)
(1); (2); (3); (4)
(1 + 2); (1 + 3); (1 + 4); (2 + 3); (2 + 4); (3 + 4)
(1 + 2 + 3); (1 + 2 + 4); (1 + 3 + 4); (2 + 3 + 4)
(1 + 2 + 3 + 4)
Essas classes, cuja construção se efetua pouco a pouco na mente do sujeito,
seja pela verificação das situações reais, seja pela dedução das combinações
possíveis, apresentam uma estrutura nova se comparada à dos agrupamentos das
operações concretas. Em outras palavras:
(...) o sistema novo que se constitui assim não é mais uma classificação simples
(nem mesmo uma vicariância entre classes das mesmas séries): é uma
classificação generalizada ou conjunto de todas as classificações possíveis
compatíveis com as associações de base que são dadas. (INHELDER;
PIAGET, 1955, p. 218).
Assim, a negação de uma combinação qualquer (por exemplo, da conjunção xy,
associação 1) não precisa mais ser construída por aproximações sucessivas por
classes complementares sob as classes mais amplas e mais próximas, como ocorre
nos agrupamentos concretos (se A é a classe dos pardais e B a dos pássaros, a
complementar escolhida pelo sujeito para A não é a negação absoluta Ā, isto é, o
conjunto das realidades que não são os pardais, mas A’, isto é, os pássaros que não
são os pardais; e se C é a classe dos animais, B‟ será a dos animais que não são
pássaros, etc.): a negação de uma combinação será o conjunto das outras, isto é, sua
complementar dentro do todo: a conjunção x ∙ y (associação 1) terá como negação x y
+ x y + x y (associação 2 + 3 + 4), ou seja, a incompatibilidade (x/y). (INHELDER;
PIAGET, 1955, p. 218).
Dessa forma, o sistema assim construído comporta ao mesmo tempo as
inversões (ou seja, as negações apresentadas no item anterior) e as reciprocidades (x
y e y x, etc.), e essas inversões e reciprocidades constituem um grupo de quatro
transformações, sendo que o sujeito não toma consciência desse grupo sob sua forma mais geral, mas que apresenta repercussões no pensamento do sujeito. (INHELDER;
PIAGET, 1955, p. 218).
_
TEXTO 121 - PARTE 25: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
101
coordenadas para obter construções livremente escolhidas e subordina as relações
causais a fins determinados. (PIAGET, 1981, p. 58).
4.3 O IMPOSSÍVEL E O NECESSÁRIO
Piaget afirma que as noções de impossível e necessário são interligadas pois a
necessidade da afirmação p equivale igualmente à impossibilidade de sua negação
não-p. (PIAGET, 1976, p. 62).
Piaget distingue três variedades de impossibilidades, conforme pode ser visto
no quadro a seguir.
Piaget afirma que essas reações são muito esclarecedoras quanto à dificuldade
das primeiras aberturas para novos possíveis:
(...) a dificuldade das novas aberturas não consiste apenas em imaginar o novo,
mas em abolir as limitações que o real opõe aos possíveis em devenir; desta
maneira, o aumento dos possíveis se apresenta também como uma vitória
progressiva, mas laboriosa, sobre as limitações. (PIAGET, 1976, p. 63-64).
Em resumo, diz Piaget, pode-se dizer que a impossibilidade subjetiva ou
pseudo-impossibilidade caracteriza-se por uma superestimação do real atual, portanto,
estados de determinados fatos, ou porque suas características particulares (na
realidade limitadas) se impõe injustificadamente como gerais e necessárias – daí as
“pseudonecessidades” – ou simplesmente porque este real atual, considerado como o
único possível, fecha as aberturas para os novos possíveis. Piaget afirma que a
negação das pseudo-impossibilidades ou pseudonecessidades não conduzem à
necessidade mas simplesmente a novas possibilidades. (PIAGET, 1976, p. 64-65).
Sobre a impossibilidade lógica Piaget diz que equivale à negação de
necessidades, e fornece o seguinte exemplo: no experimento do recorte de uma figura
quadrada, onde se pede para o sujeito imaginar quantos pedaços resultarão do recorte
de um quadrado, a criança do primeiro nível imagina que com n cortes, por exemplo
dois, obterá dois pedaços (portanto também n), ou para um só corte acredita que obterá
apenas um pedaço, desprezando o resto. Se pedir três pedaços, ela faz três cortes e
não compreende por que obtém quatro partes. “Assim, ela chega, mais ou menos
rapidamente, a descobrir a impossibilidade de obter n pedaços por meio de n cortes, o
que conduzirá à descoberta da necessidade de n cortes (n + 1) pedaços”. (PIAGET,
1976, p. 65).
Quanto às impossibilidades físicas, Piaget diz que há dois. Pode-se tratar
apenas de constatações, como no caso de um empilhamento de objetos que não
podem manter sua posição se os mais altos estão mal equilibrados, embora o sujeito
não explique estas condições de equilíbrio. Ao contrário, no caso de uma régua que
ultrapassa a borda da mesa, o sujeito consegue prever, precocemente, que é
impossível mantê-la em equilíbrio se mais da metade não estiver sobre a mesa e dá
uma explicação através do jogo de pesos, o que equivale atribuir aos objetos físicos
relações calcadas nas operações aditivas diretas e inversas. “Neste caso, a
impossibilidade física (de direito e não apenas de fato) equivale inserir o real no quadro
103
das impossibilidades e necessidades operatórias, portanto, lógico-matemáticas.”
(PIAGET, 1976, p. 65-66).
Sobre o necessário, Piaget diz que não há simples dicotomia entre o necessário
e o não-necessário, mas que existem graus variados de necessidade em função de
formas mais ou menos avançadas de equilíbrio, ou seja, de maior ou menor “força” das
estruturas. (PIAGET, 1976, p. 66).
O necessário, como o possível, é produto das composições inferenciais do
sujeito e também não é um observável. As pesquisas de Piaget e colaboradores
mostram que a evolução do necessário parece paralela à do possível, e que, nos
estágios iniciais, por haver uma indiferenciação entre factual e normativo, o real é
interpretado pelas crianças de 4-5 anos por pseudonecessidades acompanhadas de
pseudo-impossibilidades. Assim, estas formas iniciais consistem de necessidades locais devidas às composições elementares. (PIAGET, 1983, p. 8).
Piaget afirma que é possível imaginar uma grande lei de evolução que engloba o real, o possível e o necessário, conforme pode ser visto no quadro a seguir.
Um sistema é (...) um conjunto de relações interdependentes que constituem
uma totalidade com propriedades estáveis, independentemente das variações
possíveis de seus elementos. Um sistema é pois suscetível de funcionamento
sob a forma de ações ou operações momentâneas e (temporalmente)
sucessivas que modificam os elementos. Comporta, por outro lado, uma
“estrutura” enquanto conjunto intemporal das transformações possíveis que
respeitam os caracteres de sua totalidade. Chamaremos de “integração” os
processos de construção de um sistema, e “integrado” seu estado de
acabamento. A “necessitação” consistirá naquelas composições sucessivas que
tornam necessárias certas relações engendradas pelo processo integrativo (...)
e a “necessidade” caracterizará o estatuto intemporal do resultado dessas
composições quando sua negação (ou ausência) seria contraditória com as leis
da totalidade. (PIAGET, 1983, p. 8 e 44).
Mas para compreender as relações entre a necessidade e a integração, diz
Piaget, é ainda útil distinguir as três dimensões possíveis da necessidade, conforme
pode ser visto no quadro a seguir.
por si mesmas fontes de ultrapassagem, a necessitação que conduz a uma integração,
a construção de um sistema, portanto, tende a se ampliar em um novo sistema que engloba o precedente. Desse ponto de vista, uma necessidade é mais rica em
possibilidades que implica do que o sistema no seio do qual está integrada no
momento. (PIAGET, 1983, p. 44, 45). Resumindo:
(...) a integração, enquanto organizadora, é a fonte da necessitação, ao passo
que esta, enquanto estabilizadora, assegura à integração seu equilíbrio,
abrindo-a através da amplificação sobre as majorações que ela torna assim
possíveis. (PIAGET, 1983, p. 46).
Quanto ao desenvolvimento das necessidades, Piaget identificou três estágios,
conforme pode ser visto no quadro a seguir.
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
101
coordenadas para obter construções livremente escolhidas e subordina as relações
causais a fins determinados. (PIAGET, 1981, p. 58).
4.3 O IMPOSSÍVEL E O NECESSÁRIO
Piaget afirma que as noções de impossível e necessário são interligadas pois a
necessidade da afirmação p equivale igualmente à impossibilidade de sua negação
não-p. (PIAGET, 1976, p. 62).
Piaget distingue três variedades de impossibilidades, conforme pode ser visto
no quadro a seguir.
Piaget afirma que essas reações são muito esclarecedoras quanto à dificuldade
das primeiras aberturas para novos possíveis:
(...) a dificuldade das novas aberturas não consiste apenas em imaginar o novo,
mas em abolir as limitações que o real opõe aos possíveis em devenir; desta
maneira, o aumento dos possíveis se apresenta também como uma vitória
progressiva, mas laboriosa, sobre as limitações. (PIAGET, 1976, p. 63-64).
Em resumo, diz Piaget, pode-se dizer que a impossibilidade subjetiva ou
pseudo-impossibilidade caracteriza-se por uma superestimação do real atual, portanto,
estados de determinados fatos, ou porque suas características particulares (na
realidade limitadas) se impõe injustificadamente como gerais e necessárias – daí as
“pseudonecessidades” – ou simplesmente porque este real atual, considerado como o
único possível, fecha as aberturas para os novos possíveis. Piaget afirma que a
negação das pseudo-impossibilidades ou pseudonecessidades não conduzem à
necessidade mas simplesmente a novas possibilidades. (PIAGET, 1976, p. 64-65).
Sobre a impossibilidade lógica Piaget diz que equivale à negação de
necessidades, e fornece o seguinte exemplo: no experimento do recorte de uma figura
quadrada, onde se pede para o sujeito imaginar quantos pedaços resultarão do recorte
de um quadrado, a criança do primeiro nível imagina que com n cortes, por exemplo
dois, obterá dois pedaços (portanto também n), ou para um só corte acredita que obterá
apenas um pedaço, desprezando o resto. Se pedir três pedaços, ela faz três cortes e
não compreende por que obtém quatro partes. “Assim, ela chega, mais ou menos
rapidamente, a descobrir a impossibilidade de obter n pedaços por meio de n cortes, o
que conduzirá à descoberta da necessidade de n cortes (n + 1) pedaços”. (PIAGET,
1976, p. 65).
Quanto às impossibilidades físicas, Piaget diz que há dois. Pode-se tratar
apenas de constatações, como no caso de um empilhamento de objetos que não
podem manter sua posição se os mais altos estão mal equilibrados, embora o sujeito
não explique estas condições de equilíbrio. Ao contrário, no caso de uma régua que
ultrapassa a borda da mesa, o sujeito consegue prever, precocemente, que é
impossível mantê-la em equilíbrio se mais da metade não estiver sobre a mesa e dá
uma explicação através do jogo de pesos, o que equivale atribuir aos objetos físicos
relações calcadas nas operações aditivas diretas e inversas. “Neste caso, a
impossibilidade física (de direito e não apenas de fato) equivale inserir o real no quadro
103
das impossibilidades e necessidades operatórias, portanto, lógico-matemáticas.”
(PIAGET, 1976, p. 65-66).
Sobre o necessário, Piaget diz que não há simples dicotomia entre o necessário
e o não-necessário, mas que existem graus variados de necessidade em função de
formas mais ou menos avançadas de equilíbrio, ou seja, de maior ou menor “força” das
estruturas. (PIAGET, 1976, p. 66).
O necessário, como o possível, é produto das composições inferenciais do
sujeito e também não é um observável. As pesquisas de Piaget e colaboradores
mostram que a evolução do necessário parece paralela à do possível, e que, nos
estágios iniciais, por haver uma indiferenciação entre factual e normativo, o real é
interpretado pelas crianças de 4-5 anos por pseudonecessidades acompanhadas de
pseudo-impossibilidades. Assim, estas formas iniciais consistem de necessidades locais devidas às composições elementares. (PIAGET, 1983, p. 8).
Piaget afirma que é possível imaginar uma grande lei de evolução que engloba o real, o possível e o necessário, conforme pode ser visto no quadro a seguir.
Um sistema é (...) um conjunto de relações interdependentes que constituem
uma totalidade com propriedades estáveis, independentemente das variações
possíveis de seus elementos. Um sistema é pois suscetível de funcionamento
sob a forma de ações ou operações momentâneas e (temporalmente)
sucessivas que modificam os elementos. Comporta, por outro lado, uma
“estrutura” enquanto conjunto intemporal das transformações possíveis que
respeitam os caracteres de sua totalidade. Chamaremos de “integração” os
processos de construção de um sistema, e “integrado” seu estado de
acabamento. A “necessitação” consistirá naquelas composições sucessivas que
tornam necessárias certas relações engendradas pelo processo integrativo (...)
e a “necessidade” caracterizará o estatuto intemporal do resultado dessas
composições quando sua negação (ou ausência) seria contraditória com as leis
da totalidade. (PIAGET, 1983, p. 8 e 44).
Mas para compreender as relações entre a necessidade e a integração, diz
Piaget, é ainda útil distinguir as três dimensões possíveis da necessidade, conforme
pode ser visto no quadro a seguir.
por si mesmas fontes de ultrapassagem, a necessitação que conduz a uma integração,
a construção de um sistema, portanto, tende a se ampliar em um novo sistema que engloba o precedente. Desse ponto de vista, uma necessidade é mais rica em
possibilidades que implica do que o sistema no seio do qual está integrada no
momento. (PIAGET, 1983, p. 44, 45). Resumindo:
(...) a integração, enquanto organizadora, é a fonte da necessitação, ao passo
que esta, enquanto estabilizadora, assegura à integração seu equilíbrio,
abrindo-a através da amplificação sobre as majorações que ela torna assim
possíveis. (PIAGET, 1983, p. 46).
Quanto ao desenvolvimento das necessidades, Piaget identificou três estágios,
conforme pode ser visto no quadro a seguir.
TEXTO 120 - PARTE 24: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
Piaget informa que, para atingir novos possíveis, não é suficiente imaginar
processos que visam a um objetivo qualquer (com otimização ou redução a uma busca
de variações): resta compensar essa forma efetiva ou virtual de perturbação que é a
resistência do real quando concebido como “pseudonecessário”. Um tal mecanismo
provoca, aliás, esse efeito suplementar de impelir o sujeito, no momento em que
conseguiu vencer um obstáculo num ponto particular, a concluir através de uma
inferência quase evidente que, se uma variação é possível, outras o são também, a
começar pelas mais parecidas ou pelas de sentido contrário. (PIAGET, 1981, p. 9).
Se o possível procede, de um lado, das vitórias obtidas sobre o real e, por outro
lado, das lacunas a preencher quando uma variação imaginada conduz à suposição de
outras, esse duplo processo depende da equilibração em suas formas mais gerais. Mas
enquanto o sistema dos esquemas presentativos e estruturais é caracterizado por
estados de equilíbrios momentâneos ou duradouros, a natureza própria dos possíveis
abertos pelo sistema dos procedimentos é, ao contrário, sua mobilidade contínua,
reforçada pelas transferências que logo adquirem um resultado particular. (PIAGET,
1981, p. 10).
Sobre a evolução dos possíveis, Piaget faz a distinção entre possível estrutural
e funcional, conforme pode ser visto nos quadros 18 e 19.
Essa relação é tão íntima que nos foi possível utilizar os mesmos estádios para
descrever os desenvolvimentos: ao estádio pré-operatório I correspondem os
possíveis por sucessão analógica; no nível IIA, do início das operações
concretas, se constituem os co-possíveis concretos; no seguinte IIB (patamar
de equilíbrio das operações concretas) situam-se os co-possíveis que
chamaremos abreviadamente abstratos, mas simplesmente no sentido de que
são generalizados a muitos casos do que os únicos atualizados; finalmente, no
patamar III das operações hipotético-dedutivas aparecem os co-possíveis
quaisquer em um número ilimitado. (PIAGET, 1981, p. 130).
No primeiro nível, o possível engendrado gradualmente através de sucessões
analógicas, as pesquisas mostram que as primeiras aberturas para novos possíveis
decorrem de processos analógicos que combinam pequenas diferenças com
semelhanças.
No segundo nível, do co-possível concreto, os possíveis são pouco numerosos
mas todos atualizáveis (realizáveis), e no terceiro nível, do co-possível abstrato, os
possíveis são bem mais numerosos (mas não “infinitos”) e dos quais somente alguns
exemplos são fornecidos pelo sujeito. (PIAGET, 1981, p. 17). Esse qualificativo
“abstrato” significa que, para o sujeito, as poucas realizações que ele indica não são
exemplos de um campo de variações muito mais numerosas que podem ser deduzidas
enquanto totalidade, mas não realizadas (nem mesmo representadas) uma a uma.
(PIAGET, 1981, p. 25).
No último nível, do co-possível “qualquer” em número ilimitado, o possível
torna-se verdadeiramente dedutível desde a primeira constatação corrigida e isso
graças a sua união com o necessário. (PIAGET, 1981, p. 28).
Piaget afirma que o advento do co-possível não marca somente a passagem do
sucessivo ao simultâneo, o que já constitui um progresso decisivo, mas a formação de
novos tipos de possíveis que favorecem o desenvolvimento de “composições regradas”
a partir de “sobrecomposições”: esses novos tipos consistirão em relações entre
relações, ou relações entre variações, o que prepara naturalmente a formação das
operações. (PIAGET, 1981, p. 77-78).
Piaget diz que a explicação causal consiste em colocar o real num sistema de
variações co-possíveis, unidas entre si através de relações necessárias. (PIAGET,
1981, p. 28).
100
Do ponto de vista funcional, Piaget também identificou quatro níveis evolutivos
de possíveis, conforme pode ser visto no quadro a seguir.
O possível hipotético é a forma mais elementar e comporta uma mescla de
erros e de idéias fecundas que levam a êxitos. Os possíveis atualizáveis são os que,
após seleções, dão origem às realizações efetivas ou a uma idéia correta de sua
amplitude (mesmo no caso de número reconhecido “infinito”). O possível dedutível
refere-se a variações intrínsecas que podem ser inferidas a partir de uma estrutura
operatória. Por fim, fala-se de possíveis exigíveis quando o sujeito pensa que se pode e
se deve generalizar uma estrutura, mas sem saber ainda por meio de quais
procedimentos. (PIAGET, 1976, p. 62).
Piaget ainda faz a distinção entre dois tipos de possíveis: físico e instrumental.
O possível físico refere-se às possibilidades que o material oferece, mas que é preciso
descobrir através de explorações mais ou menos rudimentares ou dirigidas e que
depende da experiência. Em outras palavras, o possível físico apóia-se nos efeitos
supostamente possíveis de uma modificação determinada do material e diz respeito às
relações causais que condicionam quaisquer composições.
Já o possível instrumental refere-se aos poderes possíveis que o sujeito pode
adquirir através de suas ações apoiando-se nesse possível físico, mas ultrapassando,
mais ou menos consideravelmente, as ligações elementares e imaginando
combinações de ordem superior acompanhadas ou não de variados objetivos com fim
determinado e de uma necessidade de otimização ou, pelo menos, de melhoramentos.
Dito de outra forma, o possível instrumental apóia-se nas ações a serem executadas coordenadas para obter construções livremente escolhidas e subordina as relações
causais a fins determinados. (PIAGET, 1981, p. 58).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
Piaget informa que, para atingir novos possíveis, não é suficiente imaginar
processos que visam a um objetivo qualquer (com otimização ou redução a uma busca
de variações): resta compensar essa forma efetiva ou virtual de perturbação que é a
resistência do real quando concebido como “pseudonecessário”. Um tal mecanismo
provoca, aliás, esse efeito suplementar de impelir o sujeito, no momento em que
conseguiu vencer um obstáculo num ponto particular, a concluir através de uma
inferência quase evidente que, se uma variação é possível, outras o são também, a
começar pelas mais parecidas ou pelas de sentido contrário. (PIAGET, 1981, p. 9).
Se o possível procede, de um lado, das vitórias obtidas sobre o real e, por outro
lado, das lacunas a preencher quando uma variação imaginada conduz à suposição de
outras, esse duplo processo depende da equilibração em suas formas mais gerais. Mas
enquanto o sistema dos esquemas presentativos e estruturais é caracterizado por
estados de equilíbrios momentâneos ou duradouros, a natureza própria dos possíveis
abertos pelo sistema dos procedimentos é, ao contrário, sua mobilidade contínua,
reforçada pelas transferências que logo adquirem um resultado particular. (PIAGET,
1981, p. 10).
Sobre a evolução dos possíveis, Piaget faz a distinção entre possível estrutural
e funcional, conforme pode ser visto nos quadros 18 e 19.
Essa relação é tão íntima que nos foi possível utilizar os mesmos estádios para
descrever os desenvolvimentos: ao estádio pré-operatório I correspondem os
possíveis por sucessão analógica; no nível IIA, do início das operações
concretas, se constituem os co-possíveis concretos; no seguinte IIB (patamar
de equilíbrio das operações concretas) situam-se os co-possíveis que
chamaremos abreviadamente abstratos, mas simplesmente no sentido de que
são generalizados a muitos casos do que os únicos atualizados; finalmente, no
patamar III das operações hipotético-dedutivas aparecem os co-possíveis
quaisquer em um número ilimitado. (PIAGET, 1981, p. 130).
No primeiro nível, o possível engendrado gradualmente através de sucessões
analógicas, as pesquisas mostram que as primeiras aberturas para novos possíveis
decorrem de processos analógicos que combinam pequenas diferenças com
semelhanças.
No segundo nível, do co-possível concreto, os possíveis são pouco numerosos
mas todos atualizáveis (realizáveis), e no terceiro nível, do co-possível abstrato, os
possíveis são bem mais numerosos (mas não “infinitos”) e dos quais somente alguns
exemplos são fornecidos pelo sujeito. (PIAGET, 1981, p. 17). Esse qualificativo
“abstrato” significa que, para o sujeito, as poucas realizações que ele indica não são
exemplos de um campo de variações muito mais numerosas que podem ser deduzidas
enquanto totalidade, mas não realizadas (nem mesmo representadas) uma a uma.
(PIAGET, 1981, p. 25).
No último nível, do co-possível “qualquer” em número ilimitado, o possível
torna-se verdadeiramente dedutível desde a primeira constatação corrigida e isso
graças a sua união com o necessário. (PIAGET, 1981, p. 28).
Piaget afirma que o advento do co-possível não marca somente a passagem do
sucessivo ao simultâneo, o que já constitui um progresso decisivo, mas a formação de
novos tipos de possíveis que favorecem o desenvolvimento de “composições regradas”
a partir de “sobrecomposições”: esses novos tipos consistirão em relações entre
relações, ou relações entre variações, o que prepara naturalmente a formação das
operações. (PIAGET, 1981, p. 77-78).
Piaget diz que a explicação causal consiste em colocar o real num sistema de
variações co-possíveis, unidas entre si através de relações necessárias. (PIAGET,
1981, p. 28).
100
Do ponto de vista funcional, Piaget também identificou quatro níveis evolutivos
de possíveis, conforme pode ser visto no quadro a seguir.
O possível hipotético é a forma mais elementar e comporta uma mescla de
erros e de idéias fecundas que levam a êxitos. Os possíveis atualizáveis são os que,
após seleções, dão origem às realizações efetivas ou a uma idéia correta de sua
amplitude (mesmo no caso de número reconhecido “infinito”). O possível dedutível
refere-se a variações intrínsecas que podem ser inferidas a partir de uma estrutura
operatória. Por fim, fala-se de possíveis exigíveis quando o sujeito pensa que se pode e
se deve generalizar uma estrutura, mas sem saber ainda por meio de quais
procedimentos. (PIAGET, 1976, p. 62).
Piaget ainda faz a distinção entre dois tipos de possíveis: físico e instrumental.
O possível físico refere-se às possibilidades que o material oferece, mas que é preciso
descobrir através de explorações mais ou menos rudimentares ou dirigidas e que
depende da experiência. Em outras palavras, o possível físico apóia-se nos efeitos
supostamente possíveis de uma modificação determinada do material e diz respeito às
relações causais que condicionam quaisquer composições.
Já o possível instrumental refere-se aos poderes possíveis que o sujeito pode
adquirir através de suas ações apoiando-se nesse possível físico, mas ultrapassando,
mais ou menos consideravelmente, as ligações elementares e imaginando
combinações de ordem superior acompanhadas ou não de variados objetivos com fim
determinado e de uma necessidade de otimização ou, pelo menos, de melhoramentos.
Dito de outra forma, o possível instrumental apóia-se nas ações a serem executadas coordenadas para obter construções livremente escolhidas e subordina as relações
causais a fins determinados. (PIAGET, 1981, p. 58).
TEXTO 119 - PARTE 23: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
Elo (1978, p. 104) também apresenta curvas hipotéticas de desempenho baseadas na experiência e em capacidades orgânicas, conforme pode ser visto na figura a seguir. Enquanto que a curva de desempenho baseado na experiência somente cresce ao longo da vida, uma vez que a experiência aumenta com a idade, a curva de desempenho baseado em capacidades orgânicas tem, num primeiro momento, um
crescimento baseado em aspectos maturacionais, ocorrendo depois um declínio gradativo com o aumento da idade.
O psicólogo e grande mestre de xadrez Nicolai Krogius pesquisou a relação entre idade e desempenho no xadrez analisando a participação de 60 Grandes Mestres do passado e do presente, em 125 torneios, durante o período de 1881 a 1967. O objetivo desta pesquisa foi estabelecer, para cada jogador, o pico de sua criatividade, ou seja, o período durante o qual seus resultados foram os mais altos e consistentes. Krogius definiu o pico do jogador como a mais alta colocação nos torneios avaliados, e se o melhor resultado foi obtido várias vezes, então todos eles foram considerados. O período ótimo foi definido como o tempo, durante o qual, o grande mestre obteve os melhores resultados. (KROGIUS, 1976, p. 236).
Krogius obteve os seguintes resultados: a) o jogador de xadrez obtém seus melhores resultado com a idade aproximada de 35 anos; b) seu período de resultados ótimos duram aproximadamente 10 anos; c) este período se estende aproximadamente entre os 30 e 40 anos. (KROGIUS, 1976, p. 236). Krogius também descobriu que a idade de aprendizagem do xadrez não é um fator preponderante para definir a força do jogador, conforme pode ser visto na tabela a seguir.
segundo pico e o período ótimo é de aproximadamente 6 anos, e como regra, depois do
segundo pico um rápido declínio ocorre quando a força do jogador tem uma queda
expressiva. O segundo pico é observado principalmente em jogadores que aprenderam
o jogo relativamente tarde, depois dos 12 anos, sendo que os jogadores que
aprenderam o jogo antes dos 9 anos normalmente não apresentam o segundo pico.
Krogius argumenta que a duração do período ótimo não depende da aprendizagem
precoce do xadrez, pois métodos melhores de treinamento na adolescência podem
igualar os resultados da aprendizagem precoce. (KROGIUS, 1976, p. 240-241).
Krogius destaca que outro fator importante na carreira de um jogador é o
momento da obtenção do primeiro resultado significativo. Para pesquisar este assunto,
Krogius dividiu novamente os jogadores em dois grupos, de acordo com a idade de
aprendizagem do jogo, e então tabulou as idades em que os jogadores alcançaram o
primeiro resultado de Grande Mestre. Os dados encontram-se na tabela a seguir.
Para o período anterior à criação do título oficial de Grande Mestre, foi adotado
como resultado GM as primeiras quatro colocações em um forte torneio internacional,
ou derrotar em um match alguém que já obteve um resultado GM. (KROGIUS, 1976, p.
240).
Krogius informa que esta tabela mostra uma diferença significativa: os
jogadores do segundo grupo (que aprenderam a jogar 7 anos mais tarde) levaram 4.6
anos a menos para obter um resultado de Grande Mestre, se comparados com os
jogadores do primeiro grupo, o que fez diminuir o atraso do grupo 2 para somente 2.5
anos. Para interpretar estes resultados, Krogius (1976, p. 242) cita as opiniões oposta
de dois Grandes Mestres de xadrez sobre a aprendizagem precoce do xadrez:
Nimzowitsch e Reti. Para Nimzowitsch representa uma desvantagem em virtude da
concretude do pensamento infantil, mas para Reti, representa uma vantagem, pois
contribui para a formação e desenvolvimento da intuição no xadrez.
Krogius argumenta que se Reti estivesse certo, deveria ser encontrado um
número maior de erros graves nas partidas dos jogadores do grupo 2, pois a intuição
desempenha um importante papel na avaliação da posição imediatamente depois da
jogada do adversário. Krogius analisou então aproximadamente 1.500 partidas dos 40
Grandes Mestres selecionados da tabela 11 e encontrou erros em 4% delas. Krogius
informa que os jogadores do segundo grupo, que aprenderam a jogar mais tarde,
cometeram duas vezes mais erros do que os jogadores do grupo 1, que aprenderam a
jogar xadrez mais tarde antes. (KROGIUS, 1976, p. 241-242).
Dessa forma, destaca Krogius, os jogadores que aprendem a jogar com menos
de 10 anos fazem significativamente menos erros táticos óbvios que aqueles que
aprendem mais tarde. Isto significa que a aprendizagem do jogo precoce auxilia na
obtenção de experiências concretas que por sua vez atuam na percepção intuitiva da
posição. Assim, conclui Krogius, podemos inferir que a aprendizagem precoce do
xadrez tem um efeito definitivo para o desenvolvimento da intuição. (KROGIUS, 1976,
p. 241-243).
A seguir serão apresentados os conceitos piagetianos de real, possível,
impossível, necessário, bem como uma descrição do pensamento operatório formal.
93
4 O REAL, OS POSSÍVEIS, O IMPOSSÍVEL, O NECESSÁRIO E O PENSAMENTO
OPERATÓRIO FORMAL
Uma vez que já foi efetuada uma caracterização do jogo de xadrez, destacando
o amplo espaço de possibilidades existente nesse jogo, a seguir serão descritos os
conceitos de real, possíveis, impossível e necessário, que visam auxiliar na
compreensão de como se dá a escolha de boas jogadas durante uma partida. Na
seqüência, será feita uma descrição do período de desenvolvimento operatório formal
da inteligência, pois os participantes desta pesquisa situam-se dentro da faixa etária
que normalmente é classificada como operatório formal.
4.1 O REAL
Piaget afirma que: “o real em si mesmo, isto é, composto de objetos e de
acontecimentos conhecidos ou ainda desconhecidos, existe independentemente do
sujeito, embora só se torne conhecível à condição exclusiva de ser assimilado, portanto
interpretado por ele.” (PIAGET, 1981, p. 133).
Nesse sentido, pode-se diferenciar entre real verdadeiro e aparente: o real
verdadeiro é o que situa o dado no conjunto das possibilidades realizáveis, mas não
realizadas simultaneamente. Já o real aparente se reduz só a realidade atual, por
oposição ao possível. (BATTRO, 1971, p. 183).
Deve-se destacar que na epistemologia construtivista de Piaget, a inteligência
não inicia pelo conhecimento do eu nem pelo conhecimento das coisas, mas pela
interação dos dois. Nessa interação, a inteligência organiza o mundo organizando a si
própria. Como todo conhecimento é, ao mesmo tempo, acomodação ao objeto e
assimilação ao sujeito, a inteligência progride operando no duplo sentido da
exteriorização e interiorização, sendo seus dois pólos a experiência física (→ Y) e a
conscientização do próprio funcionamento intelectual (→ X), conforme pode ser visto na
figura a seguir.
4.2 OS POSSÍVEIS
No final da década de 1970, Piaget e colaboradores realizaram uma série de pesquisas para entender de que forma um conhecimento adquirido recentemente pode gerar novas possibilidades, produzindo novos conhecimentos. Estudaram também, de que maneira, esses novos conhecimentos tornam-se depois necessários. Em outras palavras, de que maneira se elabora a necessidade lógica e lógico-matemática. Piaget
define o possível da seguinte forma:
(...) o possível não é algo observável, mas o produto de uma construção do sujeito, em interação com as propriedades do objeto, mas inserindo-as em interpretações devidas às atividades do sujeito, atividades essas que determinam, simultaneamente, a abertura de possíveis cada vez mais
numerosos, cujas interpretações são cada vez mais ricas. (PIAGET, 1981, p. 7).
Para abordar o problema do surgimento dos possíveis, Piaget define três espécies de esquemas: presentativos, procedurais (ou de procedimentos) e operatórios. Os esquemas presentativos (e não somente representativos, pois podem
ser também sensório-motores) dizem respeito aos caracteres simultâneos dos objetos e que se conservam em caso de composição. Piaget assim define esquemas presentativos:
Chamaremos esquemas presentativos os que estão ligados às propriedades permanentes e simultâneas de objetos comparáveis. É o caso dos esquemas representativos ou conceitos (por exemplo, os ´´quadrados´´ ou os ´´gatos´´, etc.). Mas dizemos „presentativos‟ porque, além dos conceitos, esse tipo de esquema engloba igualmente um grande número de esquemas sensório-motores (por exemplo, reconhecer que um objeto está suspenso por um fio, mesmo que o bebê não o balance, ou reconhecer que um objeto está ´´afastado´´, mesmo que o sujeito não tente alcançá-lo). (PIAGET, 1976, p. 57).
Piaget afirma que os esquemas presentativos podem ser facilmente generalizados e abstraídos de seu contexto, e que se conservam mesmo se estão incluídos em outros mais amplos (como o conceito de „gato‟ incluído no de „animais‟). Os esquemas procedurais (ou de procedimentos) consistem em meios
orientados para um fim e em caso de sucessão ou de encadeamento de meios, os que serviram no início não se conservando necessariamente. No dizer de Piaget: [são] as ações sucessivas que servem de meio para alcançar um fim (por
´´precurssividade´´, isto é, determinação das ações iniciais pela orientação para um estado ulterior). Esses esquemas procedurais são difíceis de se abstrair de seus contextos, pois são, em seus detalhes, relativos a situações particulares e heterogêneas. E sua conservação é limitada, pois se um objetivo supões os meios 1, 2, 3...n, os primeiros não são mais empregados quando intervêm os
seguintes (em compensação, a evocação desses esquemas significa conserválos, mas por reconstrução presentativa). (PIAGET, 1976, p. 57-58).
Piaget destaca que os procedimentos estão ligados estreitamente ao seu contexto, sendo assim as “transferências” dos esquemas de procedimento de um
96 contexto a outros mais difíceis é bem distintas das generalizações de esquemas presentativos. (PIAGET, 1981, p. 9).
Os esquemas operatórios constituem a síntese dos dois esquemas precedentes: enquanto ato temporal e momentâneo, uma operação é um procedimento, mas a estrutura intemporal das leis de composição entre operações apresenta os
caracteres de um esquema presentativo de ordem superior. (PIAGET, 1981, p. 9).
(...) os esquemas operatórios são, de certa forma, procedurais, mas por utilização de meios regulados e gerais (as operações). Além disso, se coordenam em estruturas (uma classificação, uma seriação, etc.) que são presentativas (incluindo também o grupo de deslocamentos sensório-motor). Os esquemas operatórios constituem uma síntese dos esquemas presentativos e procedurais (e não se deve confundir esta síntese com a indiferenciação relativa dessas formas de esquemas nos níveis sensório-motores). (PIAGET, 1976, p. 58).
Assim, todo indivíduo possui dois grandes sistemas cognitivos (S1 e S2) que estão interligados e são complementares, mas de significações diferentes: um sistema
que visa compreender o real (S1), e outro destinado ao fazer e que busca o êxito (S2) em todos os domínios.
Piaget assim define fazer e compreender: “fazer é compreender em ação uma dada situação em grau suficiente para atingir os fins propostos, e compreender é
conseguir dominar, em pensamento, as mesmas situações até poder resolver os problemas por elas levantados, em relação ao porquê e ao como das ligações constatadas e, por outro lado, utilizadas na ação.” (PIAGET, 1974, p. 176).
O compreender (S1) é formado por esquemas presentativos e por esquemas operatórios enquanto estruturas. Os esquemas presentativos não permanecem isolados, mas se coordenam em classificações (para os conceitos), em seriações (para
as relações assimétricas transitivas), etc., portanto, em agrupamentos operatórios de múltiplas naturezas, inclusive os infralógicos ou espaciais (PIAGET, 1976, p. 58).
O fazer (S2, o êxito) reúne um conjunto de esquemas procedurais e os esquemas operatórios enquanto operações transformantes que visam um objetivo qualquer (solução de um problema) (PIAGET, 1976, p. 58).
97 O sistema S1 caracteriza o sujeito epistêmico, enquanto que S2 caracteriza o sujeito psicológico. (PIAGET, 1981, p. 9).
A característica principal do sistema S2 (e de todo procedimento) consiste apenas em estados de transição, pois como um procedimento visa alcançar um objetivo e, ao alcançá-lo, ele torna-se inoperante e deixa de existir enquanto procedimento:
(...) de um lado, o resultado obtido (anteriormente visado como objetivo) tornase um esquema presentativo e, de outro, se o procedimento dá lugar posteriormente a uma reconstituição mental (lembrança, compreensão das razões do êxito, etc.) é que de novo adquire, enquanto objeto conceitualizado de pensamento, um caráter presentativo. (PIAGET, 1976, p. 60).
A originalidade do sistema S2 consiste, então, em nunca estar em equilíbrio, pois é esse caráter de contínua novidade que lhe confere o papel de instrumento de reequilibrações: “visar um objetivo prático, procurar a solução de um problema, etc.; é preencher uma lacuna ou remediar incoerências e construir um novo equilíbrio, obtido
quando é alcançado ou o problema resolvido.” (PIAGET, 1976, p. 60).
Os estudos de Piaget sobre a evolução dos possíveis na criança mostram que, no início, há uma indiferenciação entre o real, o possível e o necessário, onde os objetos de conhecimento aparecem inicialmente ao sujeito, não apenas como sendo o que são, mas ainda como devendo necessariamente ser, o que exclui a possibilidade de variações ou mudanças (realidade = necessidade = única possibilidade). (PIAGET,
1981, p. 9-31).
Piaget chama essa característica de “pseudonecessidades” ou “pseudoimpossibilidades”, e acrescenta que não são exclusivas das crianças e são encontradas em todas as etapas da história das ciências.
(...) as situações de indiferenciação resultam essencialmente de insuficiência
das atividades do sujeito quanto aos possíveis e quanto à necessidade, comportando em compensação o que ele considera como real, privilégios abusivos que remedeiam essas lacunas dos poderes dedutivos: daí os bloqueios e perturbações mútuas (...). Por um lado, a formação dos possíveis é
naturalmente refreada pelas pseudonecessidades atribuídas a cada aspecto do real, mas, por outro lado, a necessidade autêntica, que repousa nos sistemas de transformação, implica uma coordenação entre os possíveis e não poderia
pois ser atingida na ausência destes. (PIAGET, 1981, p. 134).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
Elo (1978, p. 104) também apresenta curvas hipotéticas de desempenho baseadas na experiência e em capacidades orgânicas, conforme pode ser visto na figura a seguir. Enquanto que a curva de desempenho baseado na experiência somente cresce ao longo da vida, uma vez que a experiência aumenta com a idade, a curva de desempenho baseado em capacidades orgânicas tem, num primeiro momento, um
crescimento baseado em aspectos maturacionais, ocorrendo depois um declínio gradativo com o aumento da idade.
O psicólogo e grande mestre de xadrez Nicolai Krogius pesquisou a relação entre idade e desempenho no xadrez analisando a participação de 60 Grandes Mestres do passado e do presente, em 125 torneios, durante o período de 1881 a 1967. O objetivo desta pesquisa foi estabelecer, para cada jogador, o pico de sua criatividade, ou seja, o período durante o qual seus resultados foram os mais altos e consistentes. Krogius definiu o pico do jogador como a mais alta colocação nos torneios avaliados, e se o melhor resultado foi obtido várias vezes, então todos eles foram considerados. O período ótimo foi definido como o tempo, durante o qual, o grande mestre obteve os melhores resultados. (KROGIUS, 1976, p. 236).
Krogius obteve os seguintes resultados: a) o jogador de xadrez obtém seus melhores resultado com a idade aproximada de 35 anos; b) seu período de resultados ótimos duram aproximadamente 10 anos; c) este período se estende aproximadamente entre os 30 e 40 anos. (KROGIUS, 1976, p. 236). Krogius também descobriu que a idade de aprendizagem do xadrez não é um fator preponderante para definir a força do jogador, conforme pode ser visto na tabela a seguir.
segundo pico e o período ótimo é de aproximadamente 6 anos, e como regra, depois do
segundo pico um rápido declínio ocorre quando a força do jogador tem uma queda
expressiva. O segundo pico é observado principalmente em jogadores que aprenderam
o jogo relativamente tarde, depois dos 12 anos, sendo que os jogadores que
aprenderam o jogo antes dos 9 anos normalmente não apresentam o segundo pico.
Krogius argumenta que a duração do período ótimo não depende da aprendizagem
precoce do xadrez, pois métodos melhores de treinamento na adolescência podem
igualar os resultados da aprendizagem precoce. (KROGIUS, 1976, p. 240-241).
Krogius destaca que outro fator importante na carreira de um jogador é o
momento da obtenção do primeiro resultado significativo. Para pesquisar este assunto,
Krogius dividiu novamente os jogadores em dois grupos, de acordo com a idade de
aprendizagem do jogo, e então tabulou as idades em que os jogadores alcançaram o
primeiro resultado de Grande Mestre. Os dados encontram-se na tabela a seguir.
Para o período anterior à criação do título oficial de Grande Mestre, foi adotado
como resultado GM as primeiras quatro colocações em um forte torneio internacional,
ou derrotar em um match alguém que já obteve um resultado GM. (KROGIUS, 1976, p.
240).
Krogius informa que esta tabela mostra uma diferença significativa: os
jogadores do segundo grupo (que aprenderam a jogar 7 anos mais tarde) levaram 4.6
anos a menos para obter um resultado de Grande Mestre, se comparados com os
jogadores do primeiro grupo, o que fez diminuir o atraso do grupo 2 para somente 2.5
anos. Para interpretar estes resultados, Krogius (1976, p. 242) cita as opiniões oposta
de dois Grandes Mestres de xadrez sobre a aprendizagem precoce do xadrez:
Nimzowitsch e Reti. Para Nimzowitsch representa uma desvantagem em virtude da
concretude do pensamento infantil, mas para Reti, representa uma vantagem, pois
contribui para a formação e desenvolvimento da intuição no xadrez.
Krogius argumenta que se Reti estivesse certo, deveria ser encontrado um
número maior de erros graves nas partidas dos jogadores do grupo 2, pois a intuição
desempenha um importante papel na avaliação da posição imediatamente depois da
jogada do adversário. Krogius analisou então aproximadamente 1.500 partidas dos 40
Grandes Mestres selecionados da tabela 11 e encontrou erros em 4% delas. Krogius
informa que os jogadores do segundo grupo, que aprenderam a jogar mais tarde,
cometeram duas vezes mais erros do que os jogadores do grupo 1, que aprenderam a
jogar xadrez mais tarde antes. (KROGIUS, 1976, p. 241-242).
Dessa forma, destaca Krogius, os jogadores que aprendem a jogar com menos
de 10 anos fazem significativamente menos erros táticos óbvios que aqueles que
aprendem mais tarde. Isto significa que a aprendizagem do jogo precoce auxilia na
obtenção de experiências concretas que por sua vez atuam na percepção intuitiva da
posição. Assim, conclui Krogius, podemos inferir que a aprendizagem precoce do
xadrez tem um efeito definitivo para o desenvolvimento da intuição. (KROGIUS, 1976,
p. 241-243).
A seguir serão apresentados os conceitos piagetianos de real, possível,
impossível, necessário, bem como uma descrição do pensamento operatório formal.
93
4 O REAL, OS POSSÍVEIS, O IMPOSSÍVEL, O NECESSÁRIO E O PENSAMENTO
OPERATÓRIO FORMAL
Uma vez que já foi efetuada uma caracterização do jogo de xadrez, destacando
o amplo espaço de possibilidades existente nesse jogo, a seguir serão descritos os
conceitos de real, possíveis, impossível e necessário, que visam auxiliar na
compreensão de como se dá a escolha de boas jogadas durante uma partida. Na
seqüência, será feita uma descrição do período de desenvolvimento operatório formal
da inteligência, pois os participantes desta pesquisa situam-se dentro da faixa etária
que normalmente é classificada como operatório formal.
4.1 O REAL
Piaget afirma que: “o real em si mesmo, isto é, composto de objetos e de
acontecimentos conhecidos ou ainda desconhecidos, existe independentemente do
sujeito, embora só se torne conhecível à condição exclusiva de ser assimilado, portanto
interpretado por ele.” (PIAGET, 1981, p. 133).
Nesse sentido, pode-se diferenciar entre real verdadeiro e aparente: o real
verdadeiro é o que situa o dado no conjunto das possibilidades realizáveis, mas não
realizadas simultaneamente. Já o real aparente se reduz só a realidade atual, por
oposição ao possível. (BATTRO, 1971, p. 183).
Deve-se destacar que na epistemologia construtivista de Piaget, a inteligência
não inicia pelo conhecimento do eu nem pelo conhecimento das coisas, mas pela
interação dos dois. Nessa interação, a inteligência organiza o mundo organizando a si
própria. Como todo conhecimento é, ao mesmo tempo, acomodação ao objeto e
assimilação ao sujeito, a inteligência progride operando no duplo sentido da
exteriorização e interiorização, sendo seus dois pólos a experiência física (→ Y) e a
conscientização do próprio funcionamento intelectual (→ X), conforme pode ser visto na
figura a seguir.
4.2 OS POSSÍVEIS
No final da década de 1970, Piaget e colaboradores realizaram uma série de pesquisas para entender de que forma um conhecimento adquirido recentemente pode gerar novas possibilidades, produzindo novos conhecimentos. Estudaram também, de que maneira, esses novos conhecimentos tornam-se depois necessários. Em outras palavras, de que maneira se elabora a necessidade lógica e lógico-matemática. Piaget
define o possível da seguinte forma:
(...) o possível não é algo observável, mas o produto de uma construção do sujeito, em interação com as propriedades do objeto, mas inserindo-as em interpretações devidas às atividades do sujeito, atividades essas que determinam, simultaneamente, a abertura de possíveis cada vez mais
numerosos, cujas interpretações são cada vez mais ricas. (PIAGET, 1981, p. 7).
Para abordar o problema do surgimento dos possíveis, Piaget define três espécies de esquemas: presentativos, procedurais (ou de procedimentos) e operatórios. Os esquemas presentativos (e não somente representativos, pois podem
ser também sensório-motores) dizem respeito aos caracteres simultâneos dos objetos e que se conservam em caso de composição. Piaget assim define esquemas presentativos:
Chamaremos esquemas presentativos os que estão ligados às propriedades permanentes e simultâneas de objetos comparáveis. É o caso dos esquemas representativos ou conceitos (por exemplo, os ´´quadrados´´ ou os ´´gatos´´, etc.). Mas dizemos „presentativos‟ porque, além dos conceitos, esse tipo de esquema engloba igualmente um grande número de esquemas sensório-motores (por exemplo, reconhecer que um objeto está suspenso por um fio, mesmo que o bebê não o balance, ou reconhecer que um objeto está ´´afastado´´, mesmo que o sujeito não tente alcançá-lo). (PIAGET, 1976, p. 57).
Piaget afirma que os esquemas presentativos podem ser facilmente generalizados e abstraídos de seu contexto, e que se conservam mesmo se estão incluídos em outros mais amplos (como o conceito de „gato‟ incluído no de „animais‟). Os esquemas procedurais (ou de procedimentos) consistem em meios
orientados para um fim e em caso de sucessão ou de encadeamento de meios, os que serviram no início não se conservando necessariamente. No dizer de Piaget: [são] as ações sucessivas que servem de meio para alcançar um fim (por
´´precurssividade´´, isto é, determinação das ações iniciais pela orientação para um estado ulterior). Esses esquemas procedurais são difíceis de se abstrair de seus contextos, pois são, em seus detalhes, relativos a situações particulares e heterogêneas. E sua conservação é limitada, pois se um objetivo supões os meios 1, 2, 3...n, os primeiros não são mais empregados quando intervêm os
seguintes (em compensação, a evocação desses esquemas significa conserválos, mas por reconstrução presentativa). (PIAGET, 1976, p. 57-58).
Piaget destaca que os procedimentos estão ligados estreitamente ao seu contexto, sendo assim as “transferências” dos esquemas de procedimento de um
96 contexto a outros mais difíceis é bem distintas das generalizações de esquemas presentativos. (PIAGET, 1981, p. 9).
Os esquemas operatórios constituem a síntese dos dois esquemas precedentes: enquanto ato temporal e momentâneo, uma operação é um procedimento, mas a estrutura intemporal das leis de composição entre operações apresenta os
caracteres de um esquema presentativo de ordem superior. (PIAGET, 1981, p. 9).
(...) os esquemas operatórios são, de certa forma, procedurais, mas por utilização de meios regulados e gerais (as operações). Além disso, se coordenam em estruturas (uma classificação, uma seriação, etc.) que são presentativas (incluindo também o grupo de deslocamentos sensório-motor). Os esquemas operatórios constituem uma síntese dos esquemas presentativos e procedurais (e não se deve confundir esta síntese com a indiferenciação relativa dessas formas de esquemas nos níveis sensório-motores). (PIAGET, 1976, p. 58).
Assim, todo indivíduo possui dois grandes sistemas cognitivos (S1 e S2) que estão interligados e são complementares, mas de significações diferentes: um sistema
que visa compreender o real (S1), e outro destinado ao fazer e que busca o êxito (S2) em todos os domínios.
Piaget assim define fazer e compreender: “fazer é compreender em ação uma dada situação em grau suficiente para atingir os fins propostos, e compreender é
conseguir dominar, em pensamento, as mesmas situações até poder resolver os problemas por elas levantados, em relação ao porquê e ao como das ligações constatadas e, por outro lado, utilizadas na ação.” (PIAGET, 1974, p. 176).
O compreender (S1) é formado por esquemas presentativos e por esquemas operatórios enquanto estruturas. Os esquemas presentativos não permanecem isolados, mas se coordenam em classificações (para os conceitos), em seriações (para
as relações assimétricas transitivas), etc., portanto, em agrupamentos operatórios de múltiplas naturezas, inclusive os infralógicos ou espaciais (PIAGET, 1976, p. 58).
O fazer (S2, o êxito) reúne um conjunto de esquemas procedurais e os esquemas operatórios enquanto operações transformantes que visam um objetivo qualquer (solução de um problema) (PIAGET, 1976, p. 58).
97 O sistema S1 caracteriza o sujeito epistêmico, enquanto que S2 caracteriza o sujeito psicológico. (PIAGET, 1981, p. 9).
A característica principal do sistema S2 (e de todo procedimento) consiste apenas em estados de transição, pois como um procedimento visa alcançar um objetivo e, ao alcançá-lo, ele torna-se inoperante e deixa de existir enquanto procedimento:
(...) de um lado, o resultado obtido (anteriormente visado como objetivo) tornase um esquema presentativo e, de outro, se o procedimento dá lugar posteriormente a uma reconstituição mental (lembrança, compreensão das razões do êxito, etc.) é que de novo adquire, enquanto objeto conceitualizado de pensamento, um caráter presentativo. (PIAGET, 1976, p. 60).
A originalidade do sistema S2 consiste, então, em nunca estar em equilíbrio, pois é esse caráter de contínua novidade que lhe confere o papel de instrumento de reequilibrações: “visar um objetivo prático, procurar a solução de um problema, etc.; é preencher uma lacuna ou remediar incoerências e construir um novo equilíbrio, obtido
quando é alcançado ou o problema resolvido.” (PIAGET, 1976, p. 60).
Os estudos de Piaget sobre a evolução dos possíveis na criança mostram que, no início, há uma indiferenciação entre o real, o possível e o necessário, onde os objetos de conhecimento aparecem inicialmente ao sujeito, não apenas como sendo o que são, mas ainda como devendo necessariamente ser, o que exclui a possibilidade de variações ou mudanças (realidade = necessidade = única possibilidade). (PIAGET,
1981, p. 9-31).
Piaget chama essa característica de “pseudonecessidades” ou “pseudoimpossibilidades”, e acrescenta que não são exclusivas das crianças e são encontradas em todas as etapas da história das ciências.
(...) as situações de indiferenciação resultam essencialmente de insuficiência
das atividades do sujeito quanto aos possíveis e quanto à necessidade, comportando em compensação o que ele considera como real, privilégios abusivos que remedeiam essas lacunas dos poderes dedutivos: daí os bloqueios e perturbações mútuas (...). Por um lado, a formação dos possíveis é
naturalmente refreada pelas pseudonecessidades atribuídas a cada aspecto do real, mas, por outro lado, a necessidade autêntica, que repousa nos sistemas de transformação, implica uma coordenação entre os possíveis e não poderia
pois ser atingida na ausência destes. (PIAGET, 1981, p. 134).
sábado, 14 de abril de 2012
TEXTO 118 - PARTE 22: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
De Groot (1946, p. 102) diferencia dois tipos de planos no xadrez: o Plano A,
que visa o ataque, e o Plano B, que tem por objetivo a defesa. Tendo por base estes
dois tipos de planos, De Groot fornece um esquema macro estrutural do protocolo M2;
B1, assinalando o momento em que surgem estes planos, conforme pode ser visto na figura a seguir.
3.6 A EXPERTICE NO JOGO DE XADREZ.
O termo expert é geralmente empregado para definir alguém muito habilidoso e
bem informado em algum campo especial, ou para alguém amplamente reconhecido
por seus pares como uma fonte confiável de conhecimento, técnica ou habilidade.
Experts têm experiência prolongada ou intensa através de prática e estudo em um
campo particular. Expertise então se refere às características, habilidade e
conhecimento que distingue experts de novatos e de pessoas menos experientes. Em
alguns domínios, como no jogo de xadrez, há critérios objetivos para encontrar experts,
que são consistentemente capazes de exibir performance superior em tarefas
representativas em um domínio. (ERICSSON, 2006, p. 3).
Ericsson (1996, p. 6) destaca que a realização excepcional e o desempenho
são fenômenos sociais e que virtualmente cada domínio maior da expertise está
associado a uma organização hierárquica baseada em critérios sociais, onde o nível de
desempenho é tipicamente descrito pelo nível apropriado de competição envolvida
(clube, estadual, nacional, e internacional). O número de indivíduos que são admitidos
para competir em um dado nível de competição torna-se menor a medida que o nível
aumenta. Até que no nível mais alto há somente um único campeão mundial, conforme
pode ser visto na figura a seguir.
Estudos realizados com jogadores de xadrez (SIMON; CHASE, 1973) sugerem
que para se alcançar o nível internacional, é necessário por volta de 10 anos de intensa
preparação, conforme pode ser visto na figura a seguir.
FIGURA 32 – RELAÇÃO ENTRE DESEMPENHO E ANOS DE PREPARAÇÃO.
Elo (1978, p. 97), em um estudo com 36 mestres de xadrez, descreveu a curva do desenvolvimento do jogador, onde se pode observar a relação entre desempenho e
idade e perceber que o pico da carreira dos jogadores profissionais de xadrez geralmente coincide com a idade de 35 anos (veja a figura a seguir). Estudos
posteriores (ERICSSON, 1996, 56-57; ERICSSON, 2006, p. 688-689) apresentaram resultados similares aos encontrados por Elo (1978).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
De Groot (1946, p. 102) diferencia dois tipos de planos no xadrez: o Plano A,
que visa o ataque, e o Plano B, que tem por objetivo a defesa. Tendo por base estes
dois tipos de planos, De Groot fornece um esquema macro estrutural do protocolo M2;
B1, assinalando o momento em que surgem estes planos, conforme pode ser visto na figura a seguir.
3.6 A EXPERTICE NO JOGO DE XADREZ.
O termo expert é geralmente empregado para definir alguém muito habilidoso e
bem informado em algum campo especial, ou para alguém amplamente reconhecido
por seus pares como uma fonte confiável de conhecimento, técnica ou habilidade.
Experts têm experiência prolongada ou intensa através de prática e estudo em um
campo particular. Expertise então se refere às características, habilidade e
conhecimento que distingue experts de novatos e de pessoas menos experientes. Em
alguns domínios, como no jogo de xadrez, há critérios objetivos para encontrar experts,
que são consistentemente capazes de exibir performance superior em tarefas
representativas em um domínio. (ERICSSON, 2006, p. 3).
Ericsson (1996, p. 6) destaca que a realização excepcional e o desempenho
são fenômenos sociais e que virtualmente cada domínio maior da expertise está
associado a uma organização hierárquica baseada em critérios sociais, onde o nível de
desempenho é tipicamente descrito pelo nível apropriado de competição envolvida
(clube, estadual, nacional, e internacional). O número de indivíduos que são admitidos
para competir em um dado nível de competição torna-se menor a medida que o nível
aumenta. Até que no nível mais alto há somente um único campeão mundial, conforme
pode ser visto na figura a seguir.
Estudos realizados com jogadores de xadrez (SIMON; CHASE, 1973) sugerem
que para se alcançar o nível internacional, é necessário por volta de 10 anos de intensa
preparação, conforme pode ser visto na figura a seguir.
FIGURA 32 – RELAÇÃO ENTRE DESEMPENHO E ANOS DE PREPARAÇÃO.
Elo (1978, p. 97), em um estudo com 36 mestres de xadrez, descreveu a curva do desenvolvimento do jogador, onde se pode observar a relação entre desempenho e
idade e perceber que o pico da carreira dos jogadores profissionais de xadrez geralmente coincide com a idade de 35 anos (veja a figura a seguir). Estudos
posteriores (ERICSSON, 1996, 56-57; ERICSSON, 2006, p. 688-689) apresentaram resultados similares aos encontrados por Elo (1978).
TEXTO 117 - PARTE 21: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
A seguir, nas figuras 26 a 29, pode-se ver o aprofundamento progressivo do protocolo M2; B1, com as respectivas jogadas analisadas pelo mestre, bem como sua distribuição nas quatro fases no planejamento. (DE GROOT, 1946, p. 268-269).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
A seguir, nas figuras 26 a 29, pode-se ver o aprofundamento progressivo do protocolo M2; B1, com as respectivas jogadas analisadas pelo mestre, bem como sua distribuição nas quatro fases no planejamento. (DE GROOT, 1946, p. 268-269).
TEXTO 116 - PARTE 20: TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
3.5.1 Taxonomia Básica dos Planos no Jogo de Xadrez
A evolução da planificação no xadrez pode ser comparada com o que é
chamado de co-evolução em biologia onde ocorre influência evolucionária mutua entre
duas espécies, como é o caso, por exemplo, da relação entre predador e presa.
Uma águia que se alimente principalmente de um determinado tipo de preza,
como por exemplo, um coelho, contribui para a melhoria desta espécie de coelho, pois
elimina sistematicamente os indivíduos mais fracos e os restantes, que se mostram
mais aptos a sobreviverem neste ambiente, passarão seus genes adiante. A espécie de
coelhos, para não ser extinta, terá que desenvolver, dentro de um determinado tempo
evolucionário, adaptações anti-predador, como por exemplo, uma camuflagem mais
adequada ao ambiente, ou maior agilidade na fuga. Estas adaptações na espécie de
coelhos, por sua vez, poderão levar também a novas adaptações nas águias no sentido
de compensar as adaptações dos coelhos. É uma permanente corrida armamentista
entre o predador e a presa.
A evolução da planificação no ataque e na defesa no xadrez ocorre de forma
similar a co-evolução em biologia, onde um avanço no ataque leva a defesa a se tornar
mais sofisticada, o que, por sua vez, leva o ataque a refinar seus procedimentos
constantemente.
Uma abordagem psicogenética mostra que, tanto na “ontogênese” enxadrística
(evolução enxadrística individual) como na “filogênese” do xadrez (evolução do
xadrez24), a evolução da planificação segue linhas similares. Assim, uma criança que
aprende a jogar repete de certa forma, o que ocorreu na evolução do xadrez,
desenvolvendo primeiro o jogo de combinação, que é mais concreto e baseado na
tática, e depois o jogo posicional, que é mais abstrato e baseado na estratégia.
24 No item sobre a História do Xadrez pode-se acompanhar a evolução do xadrez tendo por base as
principais escolas de pensamento.
79
Nos primórdios do xadrez moderno, que surgiu no século XV, o ataque era mais
baseado em ciladas, que buscavam o ganho fácil e rápido, como é o caso do Mate do
Louco (1.f3 e5 2.g4 £h4#), do Mate do Pastor (1.e4 e5 2.¥c4 ¥c5 3.£h5 ¤f6 4.£xf7#) ou do
Mate de Legal (1.e4 e5 2.¤f3 d6 3.¥c4 ¥g4 4.¤c3 g6 5.¤xe5 ¥xd1 6.¥xf7+ ¢e7 7.¤d5#)25. Estes
ataques, assim como toda armadilha, somente têm sucesso porque o jogador que cai
na cilada não vê as reais intenções do seu adversário. Quando o jogador percebe o
perigo da posição, desenvolve esquemas defensivos visando neutralizar o ataque,
como é o caso de, no Mate do Louco, começar a partida avançando o peão do Rei duas
casas (1.e4), no Mate do Pastor, ao invés de jogar o lance 3 das pretas (3... ¤f6), jogar
3... £e7, e no Mate de Legal, ao invés de jogar o lance 4 das pretas (4... g6), jogar 4... ¤f6.
Assim, como a co-evolução entre predador e presa, os avanços na planificação do
ataque levam, por sua vez, a avanços similares no plano defensivo, como numa
interminável corrida armamentista.
O estágio atual do desenvolvimento da planificação no xadrez encontra-se
bastante avançado. Nesse sentido, Kotov (1989, p. 85) informa que os planos podem
ser para atacar, defender ou realizar qualquer vantagem, seja material ou posicional. Os
planos diferenciam-se uns dos outros por sua finalidade, seu método de realização e
sua quantidade de jogadas necessárias para alcançar o objetivo proposto.
Os planos podem ser agrupados, segundo as etapas de realização, em duas
categorias: os mono-escalonados e os multi-escalonados. Os planos mono-escalonados
são compostos de uma etapa, enquanto que os multi-escalonados por duas ou mais
etapas (KOTOV, 1989, p. 84).
Um exemplo de plano mono-escalonado vem do final rei e dama contra rei,
que pode ser formulado assim: para vencer deve-se levar o rei para a margem do
tabuleiro sem afogá-lo e aplicar o xeque-mate (KOTOV, 1989, p. 82-83).
O final de rei e torre contra rei consta de duas etapas e fornece um exemplo de
plano multi-escalonado: 1) o rei e a torre, atuando juntos, deverão restringir a liberdade
do rei adversário até que ele se encontre na margem do tabuleiro; 2) colocar o seu rei
25 Estas partidas encontram-se no CD-ROM que acompanha o volume 2, na pasta Capítulo 3. Para
visualizá-las, basta seguir as instruções do arquivo Leia-me.
80
em frente ao outro (fazendo oposição) e a torre aplicará o xeque-mate na coluna ou fila
que o rei se encontra (KOTOV, 1989, p. 83-84).
Para o ex-Campeão mundial de xadrez Garry Kasparov (KASPAROV, 2007, p.
25-26), o estrategista começa com um objetivo distante e trabalha em retrospecto até o
presente. Kasparov afirma que o Grande Mestre faz os melhores movimentos porque
eles se baseiam na aparência que ele quer que o tabuleiro tenha dez ou vinte lances à
frente. Isso não exige o cálculo de incontáveis variações das vinte jogadas. Ele avalia as
melhores possibilidades de sua posição e estabelece objetivos. Em seguida, continua
Kasparov, elabora os lances passo a passo para alcançar os objetivos. Na citação a
seguir pode-se ver a descrição de como Kasparov planeja suas ações numa
determinada posição.
Minha intuição ou análise me diz que, em uma determinada posição, existe
potencial para que eu ataque o rei do adversário. Em seguida, em vez de jogar
todas as minhas forças contra o rei, procuro objetivos que devo conquistar para
poder fazer isso com sucesso, por exemplo, enfraquecendo a proteção em
torno do rei do oponente, promovendo a troca de uma peça-chave da defesa.
Em primeiro lugar, preciso compreender que objetivos estratégicos me ajudarão
a alcançar minha meta de atacar o rei e, só então, começarei a planejar a forma
precisa de realizá-los e a examinar os lances específicos que conduzirão à
execução com bons resultados. A ausência dessa estratégia resultará em
planos simplistas com poucas chances de sucesso. (KASPAROV, 2007, p. 26).
No quadro a seguir será apresentada uma taxonomia básica dos planos no
xadrez, contendo quatro tipos de planos: 1) para obter vantagem material; 2) para obter
vantagem posicional; 3) para dar atacar o rei; e 4) para empatar a partida. Segundo o
Grande Mestre Internacional de xadrez Jaime Sunye26, o planejamento no xadrez
envolve sempre três fases principais: a) Tomada de consciência da realidade; b)
Projeções do ideal buscado; c) O caminho para alcançar o ideal buscado. Esta tabela
foi desenvolvida a partir de muitas discussões com Sunye.
26 Informação fornecida em comunicação pessoal.
3.5.2 As Fases no Planejamento no Xadrez segundo De Groot
De Groot (1946, p. 105) afirma que uma jogada possível raramente é feita
pensando somente no movimento isolado; ele quase sempre está conectado com um
objetivo mais geral ou plano que o jogador tem em mente. Assim sendo, a exploração
de um possível movimento não é um fim em si mesmo, mas antes um meio possível
para a realização de uma meta mais ambiciosa no tabuleiro: por exemplo, para obter
uma vantagem material (através de uma combinação), para realizar um ataque de
mate, para consolidar a ala da dama, e assim por diante. Esses objetivos gerais são
conhecidos na literatura enxadrística como planos e planejamento.
Para estudar as fases no planejamento, De Groot (1946, p. 91) apresentou
posições de partidas aos sujeitos que eram convidados a pensar em voz alta (thinking
aloud) e escolher a melhor continuação para a posição. Após a análise dos protocolos,
De Groot (1946, p. 267) definiu quatro fases no processo de pensamento, conforme
pode ser visto no quadro a seguir.
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
3.5.1 Taxonomia Básica dos Planos no Jogo de Xadrez
A evolução da planificação no xadrez pode ser comparada com o que é
chamado de co-evolução em biologia onde ocorre influência evolucionária mutua entre
duas espécies, como é o caso, por exemplo, da relação entre predador e presa.
Uma águia que se alimente principalmente de um determinado tipo de preza,
como por exemplo, um coelho, contribui para a melhoria desta espécie de coelho, pois
elimina sistematicamente os indivíduos mais fracos e os restantes, que se mostram
mais aptos a sobreviverem neste ambiente, passarão seus genes adiante. A espécie de
coelhos, para não ser extinta, terá que desenvolver, dentro de um determinado tempo
evolucionário, adaptações anti-predador, como por exemplo, uma camuflagem mais
adequada ao ambiente, ou maior agilidade na fuga. Estas adaptações na espécie de
coelhos, por sua vez, poderão levar também a novas adaptações nas águias no sentido
de compensar as adaptações dos coelhos. É uma permanente corrida armamentista
entre o predador e a presa.
A evolução da planificação no ataque e na defesa no xadrez ocorre de forma
similar a co-evolução em biologia, onde um avanço no ataque leva a defesa a se tornar
mais sofisticada, o que, por sua vez, leva o ataque a refinar seus procedimentos
constantemente.
Uma abordagem psicogenética mostra que, tanto na “ontogênese” enxadrística
(evolução enxadrística individual) como na “filogênese” do xadrez (evolução do
xadrez24), a evolução da planificação segue linhas similares. Assim, uma criança que
aprende a jogar repete de certa forma, o que ocorreu na evolução do xadrez,
desenvolvendo primeiro o jogo de combinação, que é mais concreto e baseado na
tática, e depois o jogo posicional, que é mais abstrato e baseado na estratégia.
24 No item sobre a História do Xadrez pode-se acompanhar a evolução do xadrez tendo por base as
principais escolas de pensamento.
79
Nos primórdios do xadrez moderno, que surgiu no século XV, o ataque era mais
baseado em ciladas, que buscavam o ganho fácil e rápido, como é o caso do Mate do
Louco (1.f3 e5 2.g4 £h4#), do Mate do Pastor (1.e4 e5 2.¥c4 ¥c5 3.£h5 ¤f6 4.£xf7#) ou do
Mate de Legal (1.e4 e5 2.¤f3 d6 3.¥c4 ¥g4 4.¤c3 g6 5.¤xe5 ¥xd1 6.¥xf7+ ¢e7 7.¤d5#)25. Estes
ataques, assim como toda armadilha, somente têm sucesso porque o jogador que cai
na cilada não vê as reais intenções do seu adversário. Quando o jogador percebe o
perigo da posição, desenvolve esquemas defensivos visando neutralizar o ataque,
como é o caso de, no Mate do Louco, começar a partida avançando o peão do Rei duas
casas (1.e4), no Mate do Pastor, ao invés de jogar o lance 3 das pretas (3... ¤f6), jogar
3... £e7, e no Mate de Legal, ao invés de jogar o lance 4 das pretas (4... g6), jogar 4... ¤f6.
Assim, como a co-evolução entre predador e presa, os avanços na planificação do
ataque levam, por sua vez, a avanços similares no plano defensivo, como numa
interminável corrida armamentista.
O estágio atual do desenvolvimento da planificação no xadrez encontra-se
bastante avançado. Nesse sentido, Kotov (1989, p. 85) informa que os planos podem
ser para atacar, defender ou realizar qualquer vantagem, seja material ou posicional. Os
planos diferenciam-se uns dos outros por sua finalidade, seu método de realização e
sua quantidade de jogadas necessárias para alcançar o objetivo proposto.
Os planos podem ser agrupados, segundo as etapas de realização, em duas
categorias: os mono-escalonados e os multi-escalonados. Os planos mono-escalonados
são compostos de uma etapa, enquanto que os multi-escalonados por duas ou mais
etapas (KOTOV, 1989, p. 84).
Um exemplo de plano mono-escalonado vem do final rei e dama contra rei,
que pode ser formulado assim: para vencer deve-se levar o rei para a margem do
tabuleiro sem afogá-lo e aplicar o xeque-mate (KOTOV, 1989, p. 82-83).
O final de rei e torre contra rei consta de duas etapas e fornece um exemplo de
plano multi-escalonado: 1) o rei e a torre, atuando juntos, deverão restringir a liberdade
do rei adversário até que ele se encontre na margem do tabuleiro; 2) colocar o seu rei
25 Estas partidas encontram-se no CD-ROM que acompanha o volume 2, na pasta Capítulo 3. Para
visualizá-las, basta seguir as instruções do arquivo Leia-me.
80
em frente ao outro (fazendo oposição) e a torre aplicará o xeque-mate na coluna ou fila
que o rei se encontra (KOTOV, 1989, p. 83-84).
Para o ex-Campeão mundial de xadrez Garry Kasparov (KASPAROV, 2007, p.
25-26), o estrategista começa com um objetivo distante e trabalha em retrospecto até o
presente. Kasparov afirma que o Grande Mestre faz os melhores movimentos porque
eles se baseiam na aparência que ele quer que o tabuleiro tenha dez ou vinte lances à
frente. Isso não exige o cálculo de incontáveis variações das vinte jogadas. Ele avalia as
melhores possibilidades de sua posição e estabelece objetivos. Em seguida, continua
Kasparov, elabora os lances passo a passo para alcançar os objetivos. Na citação a
seguir pode-se ver a descrição de como Kasparov planeja suas ações numa
determinada posição.
Minha intuição ou análise me diz que, em uma determinada posição, existe
potencial para que eu ataque o rei do adversário. Em seguida, em vez de jogar
todas as minhas forças contra o rei, procuro objetivos que devo conquistar para
poder fazer isso com sucesso, por exemplo, enfraquecendo a proteção em
torno do rei do oponente, promovendo a troca de uma peça-chave da defesa.
Em primeiro lugar, preciso compreender que objetivos estratégicos me ajudarão
a alcançar minha meta de atacar o rei e, só então, começarei a planejar a forma
precisa de realizá-los e a examinar os lances específicos que conduzirão à
execução com bons resultados. A ausência dessa estratégia resultará em
planos simplistas com poucas chances de sucesso. (KASPAROV, 2007, p. 26).
No quadro a seguir será apresentada uma taxonomia básica dos planos no
xadrez, contendo quatro tipos de planos: 1) para obter vantagem material; 2) para obter
vantagem posicional; 3) para dar atacar o rei; e 4) para empatar a partida. Segundo o
Grande Mestre Internacional de xadrez Jaime Sunye26, o planejamento no xadrez
envolve sempre três fases principais: a) Tomada de consciência da realidade; b)
Projeções do ideal buscado; c) O caminho para alcançar o ideal buscado. Esta tabela
foi desenvolvida a partir de muitas discussões com Sunye.
26 Informação fornecida em comunicação pessoal.
3.5.2 As Fases no Planejamento no Xadrez segundo De Groot
De Groot (1946, p. 105) afirma que uma jogada possível raramente é feita
pensando somente no movimento isolado; ele quase sempre está conectado com um
objetivo mais geral ou plano que o jogador tem em mente. Assim sendo, a exploração
de um possível movimento não é um fim em si mesmo, mas antes um meio possível
para a realização de uma meta mais ambiciosa no tabuleiro: por exemplo, para obter
uma vantagem material (através de uma combinação), para realizar um ataque de
mate, para consolidar a ala da dama, e assim por diante. Esses objetivos gerais são
conhecidos na literatura enxadrística como planos e planejamento.
Para estudar as fases no planejamento, De Groot (1946, p. 91) apresentou
posições de partidas aos sujeitos que eram convidados a pensar em voz alta (thinking
aloud) e escolher a melhor continuação para a posição. Após a análise dos protocolos,
De Groot (1946, p. 267) definiu quatro fases no processo de pensamento, conforme
pode ser visto no quadro a seguir.
Assinar:
Comentários (Atom)