PESQUISADO E POSTADO, PELO PROF. FÁBIO MOTTA (ÁRBITRO DE XADREZ).
REFERÊNCIA:
http://www.bibliotecadigital.unicamp.br/document/?code=000767372&opt=4
--------------------------------------------------
TESE DE DOUTORADO EM XADREZ - RACIOCÍNIO LÓGICO E O JOGO DE XADREZ: EM BUSCA DE RELAÇÕES.
AUTOR: WILSON SILVA.
ORIENTADOR: PROFº DRA. ROSELY PALERMO BRENELLI.
DATA: 23.02.2010.
4.4 A INTELIGÊNCIA OPERATÓRIA FORMAL
Para Inhelder e Piaget (1955, p. 183-184), o estudo do desenvolvimento psicológico do pensamento pode ser feito em dois pontos de vista complementares: o das condições de equilíbrio e o das condições das estruturas. Do ponto de vista das condições de equilibro, o pensamento parece, em cada uma das suas formas, passar de estados menos equilibrados a estados mais equilibrados, sendo possível identificar
dois fatores principais relativos à essa equilibração pior ou melhor: um relativo à
extensão maior ou menor do campo do equilíbrio, e o outro aos instrumentos de
coordenação, ou seja, às estruturas de que a inteligência dispõe nos níveis
considerados.
Do ponto de vista das condições das estruturas, o problema consiste em
verificar a filiação das estruturas que caracterizam essas coordenações, assim como
seu modo de construção. Essa construção depende de três fatores principais: a
maturação do sistema nervoso, a experiência adquirida em função do meio físico, e a
ação do meio social. No entanto, Piaget destaca que estes fatores só atuam, respectiva
e concorrentemente, ao se submeterem às leis de equilíbrio que determinam as
melhores formas de adaptação compatíveis com o conjunto das condições em jogo.
“Portanto, o equilíbrio e a estrutura são os dois aspectos complementares de toda
organização do pensamento.” (INHELDER; PIAGET, 1955, p. 184).
4.4.1 O pensamento formal do ponto de vista do equilíbrio
Inhelder e Piaget (1955, p. 185) destacam que a principal característica do
pensamento formal está ligada ao papel que dá ao possível com relação às verificações
de realidade, e que comparado ao pensamento concreto, constitui uma nova forma de
equilíbrio.
Ao final do período sensório-motor, por intermédio da função simbólica, uma
nova forma de pensamento se desenvolve na criança. Esta forma de pensamento é de
natureza pré-lógica (ou pré-operatória) e difere do pensamento operatório concreto sob
três aspectos: primeiro, ao considerar situações estáticas, a criança tende a explicá-las
em função de seus caracteres de configuração atual, mais do que em função das
transformações que levam de uma situação a outra. Segundo, o pensamento do sujeito,
no que se refere a essas transformações, assimila-as às ações pessoais do sujeito e
não a operações reversíveis. Estas duas diferenças podem ser reduzidas a uma: os
estados e as modificações ainda não formam, no nível do pensamento intuitivo, um sistema único, enquanto que no nível das operações concretas as situações se
subordinarão às transformações em si mesmas. Terceiro, já existe neste nível uma
tendência para a formação de sistemas de conjunto, mas a reversibilidade neste
período é ainda incompleta. (INHELDER; PIAGET, 1955, p. 185-186).
Já com o surgimento do pensamento concreto, o sistema das regulações, até
então sem estabilidade, chega a uma primeira forma de equilíbrio estável:
(...) ao atingir o nível da reversibilidade completa, as operações concretas
decorrentes das regulações precedentes se coordenam, na realidade, em
estruturas definidas (classificações, seriações, correspondências, etc.) que se
conservarão durante toda a vida, sem excluir a formação de sistemas
superiores, mas continuando ativos no plano limitado da organização dos dados
imediatos. (INHELDER; PIAGET, 1955, p. 187).
Esta forma de equilíbrio consiste, em primeiro lugar, em que os domínios
sucessivamente estruturados por esse pensamento concreto não admitem mais
oposição entre as situações estáticas e as transformações, sendo que as primeiras
subordinam-se às segundas, no sentido em que cada estado é concebido como
resultado de uma transformação.
Em segundo lugar, afirmar que o sistema das transformações está em equilíbrio
significa dizer que essas transformações adquiriram uma forma reversível e a
potencialidade para se coordenar segundo as leis fixas da composição, sendo que as
transformações são agora assimiladas às operações.
Em terceiro lugar, o pensamento operatório concreto, comparado ao
pensamento intuitivo pré-operatório, caracteriza-se por uma extensão do real na direção
do virtual, pois classificar objetos significa construir conjuntos de tal forma que novos
objetos possam ser ligados aos objetos já classificados, e novas inclusões se tornem
possíveis. Da mesma forma, seriar objetos em ordem comporta novas subdivisões
possíveis, mas estas possibilidades intrínsecas às operações concretas não estão
ainda abertas para um campo mais ou menos amplo de hipóteses, como será o caso
das operações formais. (INHELDER; PIAGET, 1955, p. 187).
(...) o pensamento concreto continua fundamentalmente ligado ao real, e o
sistema das operações concretas, que constitui a forma final de equilíbrio do
pensamento intuitivo, chega apenas a um conjunto restrito de transformações
virtuais, e, portanto, a uma noção do “possível” que é apenas uma extensão
(não muito grande) do real. Este caráter do pensamento concreto é muito claro
(...) [ao se comparar] o pensamento concreto da criança ao pensamento formal
do pré-adolescente ou do adolescente; enquanto que estes últimos, para
resolver o problema que lhes é proposto, começam imediatamente a construir
um conjunto de hipóteses entre as quais precisarão escolher
experimentalmente a melhor, a criança do nível concreto a rigor não cria
hipóteses. Age desde o começo, e apenas procura, durante sua ação,
coordenar as leituras sucessivas dos resultados que obtém, o que significa
estruturar a realidade na qual atua. Ou, se admitimos que cria hipóteses, é
preciso esclarecer que estas são apenas projetos de ações possíveis, e não,
como no adolescente, formas de imaginar o que deveria ser o real se tal ou qual
condição hipotética fosse satisfeita. (INHELDER; PIAGET, 1955, p. 188).
Inhelder e Piaget (1955, p. 189-191) apontam quatro características do
pensamento formal: inversão de sentido entre o real e o possível, o que faz com que o
pensamento formal seja essencialmente hipotético-dedutivo. O pensamento formal
refere-se a elementos verbais, e não mais diretamente aos objetos. O pensamento
formal constitui um sistema de operações de segunda potência. E por último a
utilização de um procedimento combinatório.
Com o pensamento formal ocorre uma inversão de sentido entre o real e o
possível, pois em vez de o possível se manifestar simplesmente sob a forma de um
prolongamento do real ou das ações executadas na realidade, é, ao contrário, o real
que se subordina ao possível. No pensamento formal, os fatos são concebidos como o
setor das realizações efetivas no meio de um universo de transformações possíveis,
pois não são explicados, e nem admitidos como fatos, senão depois de uma verificação
que se refere ao conjunto das hipóteses compatíveis com a situação dada.
É esta inversão de sentido entre o real e o possível que, mais que qualquer
outra propriedade subseqüente, caracteriza o pensamento formal: em vez de
apenas introduzir um início de necessidade no real, como ocorre nas
inferências concretas, realiza desde o início a síntese entre o possível e o
necessário, deduzindo com rigor as conclusões de premissas, cuja verdade
inicialmente é admitida apenas por hipótese, e, assim, vai do possível para o real. (INHELDER; PIAGET, 1955, p. 189).
Dessa forma, o pensamento formal é essencialmente hipotético-dedutivo, sendo
que a dedução não mais se refere a realidades percebidas, mas a enunciados
hipotéticos, isto é, a proposições que se referem a hipóteses ou apresentam dados
apenas como simples dados, independente do seu caráter real. Assim, a dedução
consiste em ligar estas suposições, e delas deduzir suas conseqüências necessárias,
mesmo quando sua verdade experimental não ultrapassa o possível. (INHELDER;
PIAGET, 1955, p. 189).
O pensamento formal também possui a propriedade de referir-se a elementos
verbais, e não mais diretamente aos objetos, embora nem todo pensamento verbal seja
formal. Quando os objetos são substituídos por enunciados verbais, superpõe-se uma
nova lógica – a das proposições – à das classes e relações que se referem a esses
objetos, e esta é uma segunda propriedade fundamental do pensamento formal. E esta
lógica das proposições comporta um número bem maior de possibilidades operatórias
do que os simples agrupamentos de classes e de relações. Assim, é o número de
operações possíveis que, inicialmente, a distingue funcionalmente do pensamento
concreto, pois, a prova disso é que a lógica das proposições se manifesta sob suas
formas mais características, tanto diante de situações experimentais, como diante de
problemas puramente verbais. (INHELDER; PIAGET, 1955, p. 190).
Inhelder e Piaget (1955, p. 190) destacam que o papel do pensamento formal
não se reduz a traduzir em palavras ou em proposições o que poderia ter sido
executado concretamente sem o seu recurso. Ao contrário, é durante as manipulações
experimentais que se afirma, no início do pensamento formal, uma série de
possibilidades operatórias novas, formadas por disjunções, implicações, exclusões, etc.,
que intervêm desde a organização da experiência e desde a leitura dos dados de fato.
A razão disso é que desde o contato com os problemas de fato, o pensamento formal
parte da hipótese, ou seja, do possível, em vez de limitar-se a uma estruturação direta
dos dados percebidos.
Assim, o característico da lógica das proposições não é ser uma lógica verbal.
É, antes de tudo, uma lógica de todas as combinações possíveis do pensamento, tanto
no caso em que tais combinações aparecem com problemas experimentais, quanto no caso em que aparecem diante de problemas puramente verbais.
E o motor efetivo da lógica das proposições é o poder de combinar, graças ao
qual ela insere o real no conjunto das hipóteses possíveis, compatíveis com os dados.
Inhelder e Piaget (1955, p. 190-191) destacam ainda que o pensamento formal
se constitui num sistema de operações de segunda potência. As operações concretas
são as operações de primeira potência, pois se referem diretamente aos objetos, como
por exemplo, a construção de relações entre elementos dados. No entanto, também é
possível construir relações entre relações, como por exemplo, as proporções, cuja
conquista só é obtida no nível formal, sendo que as proporções supõe as operações de
segunda potência.
Esta noção de operação de segunda potência exprime novamente o caráter
geral do pensamento formal, que é o de ultrapassar o quadro das
transformações que se referem diretamente ao real (operações de primeira
potência) subordinando-as a um sistema de combinações hipotético-dedutivas,
e, portanto, simplesmente possíveis. (INHELDER; PIAGET, 1955, p. 191).
Por fim, Inhelder e Piaget destacam o caráter combinatório do pensamento
formal, pois para lidar com o possível, o sujeito precisa de um instrumento para gerá-lo,
e esse instrumento é uma combinatória, um procedimento para combinar elementos
que, diante de uma situação determinada, permite ao sujeito a produção de todos os
casos possíveis. Inhelder e Piaget afirmam que “apenas uma combinação dá o conjunto
dos possíveis e, no terreno experimental, a pesquisa das combinações novas é
precisamente o que caracteriza a hipótese.” (1955, p. 191). Ver quadro 24.
QUADRO 24 – CARACTERÍSTICAS DO PENSAMENTO FORMAL.
Do ponto de vista físico, sabe-se que um estado de equilíbrio se caracteriza pela compensação entre todas as modificações virtuais, compatíveis com as ligações
do sistema considerado. No dizer de Inhelder e Piaget (1955, p. 193):
(...) para conceber o possível, o pensamento formal é obrigado a dispor, em cada situação específica, de uma grande amplitude de operações virtuais que ultrapassam o domínio das operações momentaneamente utilizadas de fato, e
tais operações virtuais constituem uma condição necessária de equilíbrio, e isso, pelas duas razões seguintes: de um lado, são elas que correspondem ao que na linguagem da teoria do equilíbrio, denominamos as “transformações virtuais”; de outro, há equilíbrio na medida em que essas transformações virtuais “se
compensam” exatamente, ou, na linguagem das operações, na medida em que tais operações possíveis constituem um sistema rigorosamente reversível do
ponto de vista lógico.
Do ponto de vista lógico, a significação lógica representa um caráter indispensável para o funcionamento do pensamento hipotético-dedutivo ou formal.
Deve-se ter em mente que, na realidade, o possível formal é o correlato obrigatório, de noção e de necessidade.
Inhelder e Piaget (1955, p. 193) destacam que:
Uma afirmação relativa apenas ao real – por exemplo, um juízo de existência ou um juízo predicativo – não precisa ser necessário: a afirmação é verdadeira ou falsa, na medida em que corresponde ou não a um fato. Uma dedução que refere a uma hipótese (ou a um dado de fato, mas admitido como hipótese), é, ao contrário, necessariamente verdadeira, do ponto de vista formal, desde que seja correta, e isso independentemente do valor da hipótese admitida. A
conexão marcada pelas palavras “se...então” (implicação inferencial) consiste em ligar uma conseqüência necessária a uma afirmação simplesmente possível: é esta síntese do necessário e do possível que caracteriza o emprego desse possível no pensamento formal, por oposição ao possível extensão-doreal do pensamento concreto e às possibilidades não reguladas, características das ficções da imaginação.
Inhelder e Piaget (1955, p. 193-194), ao indagar em que consiste este possível formal, argumentam “é possível tudo que não é contraditório”. Assim, a reversibilidade operatória formal que, na perspectiva física significa a exata compreensão das transformações (ou operações) virtuais, adquire na perspectiva lógica, a significação da
necessidade dedutiva.
No conjunto, esses dois aspectos, físico e lógico, da noção de possível,
psicologicamente constituem apenas um: ao situar um estado real num sistema
de transformações possíveis, o pensamento formal assegura, simultaneamente,
seu equilíbrio, do ponto de vista da conservação psicológico ulterior das
estruturas que desenvolve, e seu valor de instrumento lógico necessário, do
ponto de vista da utilização dessas estruturas, enquanto instrumentos
dedutivos. (INHELDER; PIAGET, 1955, p. 194).
Inhelder e Piaget (1955, p. 195) apontam duas significações psicológicas para a
palavra possível: o materialmente possível e o estruturalmente possível. O
materialmente possível é o possível do ponto de vista do sujeito, e refere-se às
operações ou relações que o sujeito concebe como possível, ou seja, aquilo que o
sujeito sabe que pode efetuar ou construir, mesmo que não o faça efetivamente. O
estruturalmente possível é o possível do ponto de vista do observador, e são as
operações e relações que o sujeito seria capaz de efetuar ou de construir, mas sem que
pense fazê-lo, ou seja, sem que tome consciência dessa eventualidade, nem de sua
capacidade a respeito. Inhelder e Piaget (1955, p. 196) destacam que:
(...) sempre devem ser consideradas, num ato de inteligência, as operações
reais, no sentido de efetivamente realizadas no pensamento consciente do
sujeito, e as operações “estruturalmente possíveis”, isto é, que não efetua, mas
que poderia efetuar. (...) é esse possível relativo às estruturas operatórias, de
que o sujeito dispõe, que constitui o possível do ponto de vista do observador e
que, portanto, corresponde, no domínio físico, às transformações virtuais, não
efetivamente realizadas.
O materialmente possível tem estreitas relações com o estruturalmente
possível, do qual constitui um primeiro plano de atualização: é na medida em que o
sujeito dispõe de um número suficiente de operações estruturalmente possíveis que
chega a imaginar as transformações materialmente possíveis. No dizer de Inhelder e
Piaget:
Sem um certo jogo de possibilidades estruturais (e é o que se manifesta
claramente ao nível pré-operatório, e mesmo no das operações concretas), não
poderia verificar os estados de fatos percebidos no real, os estados estáticos ou
as transformações atuais, e não chegaria a ter uma representação das
transformações hipotéticas que servem para que imagine novas experiências.
Portanto, o materialmente possível depende do estruturalmente possível.
(INHELDER; PIAGET, 1955, p. 196).
114
4.4.2 O pensamento formal do ponto de vista das Estruturas
Depois de caracterizar a diferença entre o pensamento concreto e pensamento
formal do ponto de vista do equilíbrio, por intermédio da extensão progressiva do
conjunto das operações virtuais ou possíveis, Inhelder e Piaget destacam que é
necessário comparar as estruturas totais que correspondem a essas duas formas de
equilíbrio.
Inhelder e Piaget (1955, p. 205) afirmam que todo estado de equilíbrio pode ser
reconhecido por uma certa forma de reversibilidade. Do ponto de vista estrutural, a
reversibilidade, que é a possibilidade permanente de uma volta ao ponto de partida, se
apresenta sob duas formas distintas e complementares. Pode-se voltar ao ponto de
partida anulando-se a operação efetuada, o que constitui uma inversão ou negação: o
produto da operação direta e de seu inverso é a operação nula ou idêntica. Mas
também se pode voltar ao ponto de partida anulando uma diferença (no sentido lógico
do termo), o que constitui uma reciprocidade: o produto de duas operações recíprocas
é, não uma operação nula, mas uma equivalência.
A inversão e a reciprocidade são encontradas sob aspectos diferentes em todos
os estádios de desenvolvimento, pois constituem as condições de equilíbrio das
ações mais elementares, bem como das ações superiores. É assim que no nível
perceptivo (embora não exista ainda nenhuma reversibilidade completa) as
inversões correspondem às adjunções ou supressões de elementos e as
reciprocidades às simetrias ou semelhanças. (INHELDER; PIAGET, 1955, p.
205).
Existe uma primeira diferença importante entre as estruturas concretas e
formais: enquanto que as segundas chegam a reunir as inversões e as reciprocidades
em um sistema único de transformações (o grupo INRC), os sistemas característicos
das operações concretas, ou agrupamentos de classes e de relações, decorrem da
inversão (classes) ou da reciprocidade (relações), sem síntese geral dessas duas
formas de reversibilidade. (INHELDER; PIAGET, 1955, p. 205-206).
115
De uma maneira geral, os “agrupamentos” elementares, que constituem as
únicas estruturas de conjunto acessíveis ao nível das operações concretas, se
caracterizam, portanto, por duas particularidades essenciais que as opõe às
estruturas formais: 1) Constituem sistemas de inclusões ou de encadeamentos
simples ou múltiplos, mas sem combinatória que inclua uma combinatória que
ligue os diversos elementos de n por n; por conseguinte não atingem a estrutura
do reticulado que comporta uma tal combinatória (“conjunto das partes”), mas
permanecem no estado de semi-reticulados; 2) Apresentam uma reversibilidade
que consiste seja em inversão (classes), seja em reciprocidade (relações), mas
não chegam a reunir essas duas formas de reversibilidade num sistema único;
por isso, não coincidem com a estrutura do grupo das inversões e
reciprocidades (o grupo INRC) e permanecem no estado de grupos
incompletos. (INHELDER; PIAGET, 1955, p. 207).
As estruturas concretas de classes consistem exclusivamente de classificações
simples (aditivas) ou multiplicativas (tabelas multiplicativas ou matrizes), de tal forma
que cada classe depende daquelas de que faz parte (A incluído em B, B em C, etc.) e
se opõe à sua complementar com relação à classe imediatamente superior (A‟ = B – A :
B‟ = C – B; etc.), mas sem combinatória que dê todos os sub-conjuntos possíveis de
classes no interior do sistema. Essas estruturas repousam exclusivamente na
reversibilidade por inversão: o sujeito pode assim reunir duas classes contíguas numa
única classe (A + A‟ = B; etc.) ou subtrair uma do todo assim formado (A = B – A‟); pode
também multiplicar uma classe pela outra (A1 x A2 = A1A2) ou abstrair uma do todo
assim formado (A1A2 : A2 = A1); mas tais sistemas ignoram a forma geral da
reciprocidade. (INHELDER; PIAGET, 1955, p. 206).
Inhelder e Piaget afirmam que as estruturas concretas de relações coordenam
entre si as equivalências completas (igualdades) ou parciais (alteridades) no caso de
relações simétricas, as diferenças ordenadas no caso das relações assimétricas
transitivas (seriações ou encadeamentos) e comportam igualmente os sistemas
multiplicativos (correspondências, etc.). A reversibilidade característica dessas
estruturas consiste de reciprocidades.
Para se entender a capacidade da inteligência operatória formal convém
compará-la com os agrupamentos mais complexos de que a inteligência operatória
concreta é capaz: as classificações multiplicativas (matrizes). Piaget e Inhelder (1959,
p. 188) fornecem o exemplo: dado um jogo de elementos de duplas características
(quadrados e círculos, vermelhos e azuis) que podem ser repartidos em duas classes
116
A1 e A‟1, segundo uma das suas características (A1= quadrados e A‟1= círculos) e,
igualmente, em duas classes A2 e A‟2, segundo a outra característica (A2= vermelhos e
A‟2= azuis), chama-se B1 à reunião das duas primeiras classes (formas), ou seja, B1= A1
+ A‟1, e B2 à reunião das duas segundas (cores), ou seja, B2= A2 + A‟2.
A classificação multiplicativa consiste em classificar esses elementos ao mesmo
tempo, segundo a classificação aditiva B1 e segundo a classificação aditiva B2, o que
originará quatro classes distintas: A1 A2+ A1 A‟2 + A‟1 A2 + A‟1 A‟2. Para resolver o
problema o sujeito deve, necessariamente, construir uma matriz de duas dimensões
(quadro de dupla entrada m n), como pode ser visto a seguir:
QUADRO 25 – MATRIZ DE DUPLA ENTRADA.
(...) o que falta às estruturas concretas de agrupamento é a combinatória intrínseca à construção do “conjunto das partes”, ou, o que é a mesma coisa, é a utilização de operações proposicionais (implicação, etc.) ou isomórficas
destas últimas, pois as operações interproposicionais repousam sobre a estrutura desse “conjunto das partes”. A diferença entre os agrupamentos elementares de classes e de relações (classificações, seriações e correspondências multiplicativas) e esta estrutura é que os primeiros constituem somente remi-reticulados, enquanto que o conjunto das partes forma um reticulado completo. Em segundo lugar, as operações com o “conjunto das partes” comportam uma inversa e uma recíproca: a segunda diferença essencial
entre os agrupamentos concretos e o sistema de operações formais refere-se, então, à ausência de um grupo único que ligue as inversões e reciprocidades nos agrupamentos elementares, bem como a presença desse grupo logo que se constitui o “conjunto das partes”. (INHELDER; PIAGET, 1955, p. 207).
Inhelder e Piaget destacam que não é suficiente assinalar estas diferenças entre as operações concretas e formais, mas de compreender o que leva o sujeito, por volta de 11 ou 12 anos, a construir efetivamente os “conjuntos das partes”. Com o objetivo de identificar em que casos os sujeitos utilizavam ou não as operações proposicionais, Inhelder e Piaget afirmam que “é quase impossível, diante de um
enunciado isolado qualquer, decidir entre essas duas possibilidades, e a questão não apresenta significação psicológica a não ser em função do conjunto dos raciocínios do sujeito ou de uma seqüência suficientemente sistemáticas de inferências.” Portanto, a linguagem dos sujeitos não traduz, senão de uma maneira muito aproximada, a estrutura real de seus pensamentos. (INHELDER; PIAGET, 1955, p. 209-210).
Inhelder e Piaget (1955, p. 210) propõem que é mais adequado comparar todos os enunciados, e, sobretudo todas as ações de um mesmo sujeito. Assim, pode-se ver se o sujeito se limita a uma simples leitura dos resultados brutos da experiência para destes extrair apenas classificações, seriações ou correspondências, ou se tenta dissociar os fatores, o que implica, ao mesmo tempo, um raciocínio hipotético-dedutivo
e uma combinatória.
Inhelder e Piaget destacam que a passagem das operações concretas para as operações formais não ocorre por um salto brusco, mas sim por múltiplas transições que o sujeito vai passar desde o nível da simples leitura dos fatos brutos, por meio de classificações, seriações e correspondências, para o nível da combinatória. Ao indagar sobre por que o equilíbrio final das operações combinatórias é tão
tardio, Inhelder e Piaget afirmam que:
(...) na medida em que as operações derivam umas das outras por coordenações progressivas, e em que as mais simples procedem da ação irreversível, compreendemos as razões pelas quais o equilíbrio das operações
combinatórias é tão tardio: o sujeito deve, inicialmente, dessubjetivar suas
ações para torná-las reversíveis, o que equivale a coordená-las em agrupamentos elementares ainda próximos da manipulação, e depois, como não consegue imediatamente dissociar inteiramente a forma e o conteúdo, é obrigado a reconstruir esses diversos agrupamentos nos domínios heterogêneos sucessivos que lhe impõe a experiência; é somente depois dessa estruturação progressiva dos diferentes conteúdos da experiência que um mecanismo formal geral começa a ser isolado por coordenação de conjunto. (INHELDER; PIAGET, 1955, p. 211).
Inhelder e Piaget destacam que enquanto as operações concretas procedem conteúdo por conteúdo, a realidade cedo ou tarde impõe uma mistura de conteúdos, forjando novos instrumentos operatórios. Dois métodos são então empregados pelo sujeito: no primeiro, o sujeito procura coordenar entre si os resultados das operações concretas, ou seja, eliminar as contradições aparentes; no segundo, o sujeito procura
coordenar diretamente entre si as diversas operações características dos agrupamentos concretos. Inhelder e Piaget assinalam que esses dois métodos conduzem à
descoberta da lógica formal das proposições, que consistem em: 1) Dissociar os conteúdos estruturados apenas pelas operações concretas, de maneira a coordenar os resultados dessas operações, em função das diversas combinações possíveis; 2) Coordenar os diversos agrupamentos de classes e de relações num único sistema total. Esses dois processos, por mais diferentes que possam parecer entre si, na realidade se reduzem a um só, pois os dois repousam numa combinatória. (INHELDER; PIAGET, 1955, p. 212).
No nível das operações concretas o sujeito procura estruturar a realidade de maneira mais completa que lhe é acessível, mas se limita ao real sob sua forma bruta.
A razão para isso é que as operações concretas (entre os 7 e 12 anos) têm por função estruturar o real, domínio por domínio, considerando esses conteúdos um após o outro,
às vezes com intervalo de alguns anos entre eles, como no caso das decalagens.
(...) quanto mais o sujeito analisa concretamente (portanto por simples correspondências entre os conteúdos distintos) a realidade, mais esta lhe apresenta misturas de regularidades parciais e exceções, e que não podem ser interpretadas com segurança. Inicialmente, é natural que o sujeito despreze,
seja as regularidades parciais, seja, principalmente, as exceções; mas, quando começa a levar a sério as exigências da experiência, encontra-se diante de uma situação sem saída do ponto de vista da simples descrição concreta dos fatos
brutos. (INHELDER; PIAGET, 1955, p. 213).
Inhelder e Piaget destacam que, cedo ou tarde, se impõe uma nova atitude experimental, que se pronuncia em numerosos casos desde o nível concreto, mas não
se generaliza antes do nível formal: é a tentativa de dissociar os fatores. Para compreender em que consiste essa tentativa de dissociar os fatores, deve-se analisar:
sob que formas nasce essa tentativa; sob que formas se generaliza e porque se generaliza tardiamente; como conduz necessariamente a uma combinatória. (INHELDER; PIAGET, 1955, p. 213).
No nível concreto, já existem algumas formas de dissociação de fatores, pois, tratando de decidir se determinado fator desempenha um papel ou não no resultado dado, o sujeito desse nível já é capaz de alguns processos, alguns por observação pura, outros por experimentação. Inhelder e Piaget informam que nesses dois casos (observação ou experimentação), a dissociação dos fatores, característica do nível concreto, é uma dissociação por negação, ou seja, o fator cujo papel é discutido às vezes está presente, às vezes ausente (observação) ou então é introduzido ou afastado
(experimentação). Portanto, tem-se aí exclusivamente transformações por inversão ou negação, e não reciprocidades; assim, tem-se a primeira e não as duas formas de reversibilidade.
Uma segunda diferença entre as dissociações elementares do nível das operações concretas e a dissociação do nível das operações formais é que, no caso de
dois ou vários fatores, x, y, etc., o sujeito não introduz e nem elimina o fator x a não ser para ver se desempenha sozinho um papel ativo, e não para estudar as variações de y.
Os sujeitos do nível formal, ao contrário, afastarão um fator x, e não somente para controlar sua influência, mas também para analisar a de y, sem perturbação por parte
de x. (INHELDER; PIAGET, 1955, p. 213-214).
As duas descobertas características do início do nível formal são que o sujeito pode dissociar fatores por neutralização, assim como por exclusão, e que é necessário
afastar um fator, não somente para analisar sua ação, mas ainda para mostrar a de outros fatores presentes. No dizer de Inhelder e Piaget:
É então que aparece a conduta característica do nível III [formal], que consiste em, diante de associações x, y, afastar y para estudar x sem interferências
perturbadoras, e reciprocamente. Portanto, a necessidade de excluir um fator para fazer variar um outro nasce de uma inversão de sentido na construção de correspondências, tendendo a abstrair ou a dissociar, em vez de multiplicar ou
associar, e isso diante da excessiva complexidade e das contradições que caracterizam a experiência bruta. Diante disso, alguns fatores podem ser afastados por inversão ou negação, mas isso não ocorre com todos. A segunda novidade característica do estádio III consiste em generalizar esta exclusão dos fatores perturbadores no caso em que tais fatores não comportam negação: neste caso o que é negado não é mais um dos termos (propriedade ou acontecimento), mas a diferença entre eles. Em outras palavras, o fator que
deve ser excluído é simplesmente neutralizado por igualização dos termos existentes, o que constitui uma reciprocidade, e não mais uma inversão. (INHELDER; PIAGET, 1955, p. 214-215).
Inhelder e Piaget afirmam que a dissociação de fatores, característica do nível formal, introduz uma reversibilidade por reciprocidade, ao mesmo tempo que por inversão, ao utilizar, de maneira paralela, as duas formas de reversibilidade, e ao tornálas funcionalmente equivalentes.
Inhelder e Piaget destacam que ainda é necessário mostrar como estas duas novidades trazem consigo, necessariamente, a constituição de uma combinatória. Logo que o sujeito ingressa no caminho de uma dissociação de fatores, ele se encontra diante de novas possibilidades. Em uma situação experimental realizada, o sujeito deveria descobrir se a flexibilidade de uma haste de metal depende do material que é
feita, de seu comprimento, de sua grossura ou de sua forma de corte. Inhelder e Piaget, ao analisar os resultados, apontam que:
(...) de início [o sujeito] associa todos esses fatores entre si por comparação 2
por 2, 3 por 3, etc.; mas isso não ultrapassa as operações multiplicativas do nível concreto (tabelas com 2, 3, ...entradas) e verificamos que essas associações ou correspondências multiplicativas continuam insuficientes para
solução dos problemas, ainda que seja necessário começar pelo seu estabelecimento. Apenas depois, quando essas associações de base já foram construídas, é que entre as combinações possíveis devem ser escolhidas as
combinações que permitem uma comprovação. Portanto, é aqui que aparece necessariamente a combinatória. (INHELDER; PIAGET, 1955, p. 215).
Inhelder e Piaget afirmam que se pode pensar que desses fatores associados cada um atue separadamente, enquanto os outros são conservados invariáveis, e a combinação comprobatória é aquela que faz variar apenas um fator. No entanto, também é possível pensar que dois ou três deles devam intervir simultaneamente para provocar o efeito observado. Também pode ocorrer que haja intervenção de um ou outro, mas cada um com exclusão do outro, ou um em sentido inverso ao do outro. Portanto, é evidente que a dissociação dos fatores chega, segundo o caso, a um certo número de possibilidades distintas que se traduzem por implicações,
equivalências, disjunções, conjunções, exclusões, incompatibilidades, etc. (...).
Numa palavra, a dissociação dos fatores chega necessariamente a combinar entre si, n por n, as associações de base, e, portanto, a substituir as simples operações de multiplicação ou de correspondência, que criaram essas
associações de base, pela combinatória característica do “conjunto das partes”. (INHELDER; PIAGET, 1955, p. 215-216).
Inhelder e Piaget (1955, p. 216), após verificar que a dissociação dos fatores, que ocorre pela necessidade de coordenar entre si os resultados mais complexos das
operações concretas de estabelecimento de relações e correspondências, leva necessariamente a uma combinatória, assinalam que é necessário mostrar como esta
combinatória engendra o pensamento formal. Inhelder e Piaget destacam que é necessário saber de que forma a coordenação das operações concretas chega à combinatória inerente à lógica das proposições e, portanto, ao pensamento formal.
Uma vez que o sujeito classifica, seria, iguala, coloca em correspondência, etc., os diversos aspectos da situação que condicionam a solução de um problema, para resolver o problema pode ser necessário reunir num único sistema as operações até então realizadas, e é a isso que conduz a necessidade de coordenar entre si seus resultados, quando são insuficientemente coerentes. Ora, não há operações que permitam ligar diretamente os diversos agrupamentos de classes e relações num único sistema, sem sair de inclusões
simples, aditivas ou multiplicativas, e, portanto, sem construir seu “conjunto das partes”, isto é, justamente essa combinatória cuja formação no pensamento espontâneo dos sujeitos precisamos agora compreender. (INHELDER; PIAGET,
1955, p. 216).
Inhelder e Piaget informam que, seja para as classes ou para as relações (mas não para as duas coisas ao mesmo tempo), há um agrupamento mais geral que os outros, no sentido que os contém ou em que tais agrupamentos dele derivam por
especificações sucessivas. O agrupamento concreto mais geral é o agrupamento multiplicativo (de classes ou relações) que consiste de tabelas de dupla entrada (ou tripla, etc.). Nesta forma de agrupar os dados, para dois acontecimentos ou
propriedades (x e y), o sujeito constrói associações elementares xy + x y + x y + x y . Assim, novos problemas se apresentam para o sujeito, que precisa decidir quais, entre
essas associações são verdadeiras, e qual é a significação que deve ser atribuída a esses subconjuntos.
É muito interessante verificar que a escolha ou essa verificação dos
subconjuntos de associações verdadeiras, entre as possibilidades xy + x y + x
y + x y , se devem a simples operações de classificação, mas aplicadas às
associações (xy, etc.) e generalizadas a todos os casos possíveis: o sujeito
reúne assim os casos xy aos casos x y , ou o caso xy ao caso x y , etc., como
se se tratasse de uma reunião de objetos qualificados por suas propriedades
comuns, quando, na realidade, se trata de reunir as associações, isto é, as
situações nas quais duas propriedades se apresentam juntas (ou uma sem a
outra, etc.) ou ainda, onde dois acontecimentos se produzem ao mesmo tempo
(ou um sem o outro, etc.). Em outros termos, o sujeito, partindo do conjunto
multiplicativo xy + x y + x y + x y , constrói seu “conjunto de partes” através de
uma nova classificação: portanto, aplica o mais simples dos agrupamentos (a
classificação) ao mais geral (a tabela das multiplicações lógicas), chegando
assim a uma espécie de agrupamento de segunda potência que coordenará
todos os agrupamentos num sistema superior, uma vez que não pode ligá-los
diretamente entre si. (INHELDER; PIAGET, 1955, p. 216-217).
Inhelder e Piaget assinalam que esse agrupamento de segunda potência, por aplicação da classificação generalizada às associações multiplicativas, não é mais do que uma combinatória n por n, e podem-se extrair as seguintes conseqüências quanto à elaboração do pensamento formal:
Em primeiro lugar, essa classificação generalizada das associações xy, etc., chega a um novo modo de composição. Inhelder e Piaget (1955, p. 217) destacam que as classificações anteriormente utilizadas pelo sujeito eram essencialmente formas de inclusão simples (por exemplo, rouxinol < pássaro < animal < ser vivo), de acordo com
o mais elementar dos agrupamentos: A + A‟ = B; B + B‟ = C; etc., ou ainda, as classificações segundo dois critérios possíveis (os genebrinos mais os outros suíços =
os valdenses mais os outros suíços), ou seja, A1 + A‟1 = A2 + A‟2, etc. (vicariância).
Quando se trata de uns nos outros os subconjuntos de associações num agrupamento multiplicativo, levando em consideração as diferentes possibilidades, o modo de
composição será muito diverso e chegará a uma combinação n por n por generalização da vicariância.
Por exemplo, dado os elementos x e y, as quatro associações possíveis podem ser representadas pelos números de 1 a 4:
_ _ ___
1 = xy; 2 = x y ; 3 = x y e 4 = x y
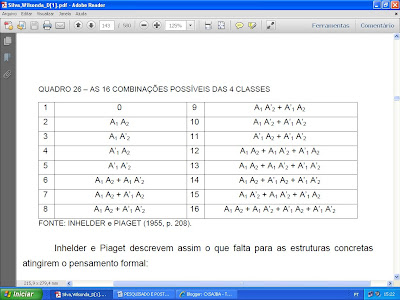
As classes resultantes das inclusões possíveis serão 16 (veja o quadro 26):
(0)
(1); (2); (3); (4)
(1 + 2); (1 + 3); (1 + 4); (2 + 3); (2 + 4); (3 + 4)
(1 + 2 + 3); (1 + 2 + 4); (1 + 3 + 4); (2 + 3 + 4)
(1 + 2 + 3 + 4)
Essas classes, cuja construção se efetua pouco a pouco na mente do sujeito,
seja pela verificação das situações reais, seja pela dedução das combinações
possíveis, apresentam uma estrutura nova se comparada à dos agrupamentos das
operações concretas. Em outras palavras:
(...) o sistema novo que se constitui assim não é mais uma classificação simples
(nem mesmo uma vicariância entre classes das mesmas séries): é uma
classificação generalizada ou conjunto de todas as classificações possíveis
compatíveis com as associações de base que são dadas. (INHELDER;
PIAGET, 1955, p. 218).
Assim, a negação de uma combinação qualquer (por exemplo, da conjunção xy,
associação 1) não precisa mais ser construída por aproximações sucessivas por
classes complementares sob as classes mais amplas e mais próximas, como ocorre
nos agrupamentos concretos (se A é a classe dos pardais e B a dos pássaros, a
complementar escolhida pelo sujeito para A não é a negação absoluta Ā, isto é, o
conjunto das realidades que não são os pardais, mas A’, isto é, os pássaros que não
são os pardais; e se C é a classe dos animais, B‟ será a dos animais que não são
pássaros, etc.): a negação de uma combinação será o conjunto das outras, isto é, sua
complementar dentro do todo: a conjunção x ∙ y (associação 1) terá como negação x y
+ x y + x y (associação 2 + 3 + 4), ou seja, a incompatibilidade (x/y). (INHELDER;
PIAGET, 1955, p. 218).
Dessa forma, o sistema assim construído comporta ao mesmo tempo as
inversões (ou seja, as negações apresentadas no item anterior) e as reciprocidades (x
y e y x, etc.), e essas inversões e reciprocidades constituem um grupo de quatro
transformações, sendo que o sujeito não toma consciência desse grupo sob sua forma mais geral, mas que apresenta repercussões no pensamento do sujeito. (INHELDER;
PIAGET, 1955, p. 218).
_










Nenhum comentário:
Postar um comentário